5.5. Excited State Dynamics

ORCA can now also be used to compute dynamic properties involving excited states such as absorption spectra, fluorescence and phosphorescence rates and spectra, as well as resonant Raman spectra using the new ORCA_ESD module. We do this by analytically solving the Fermi’s Golden Rule-like equation from Quantum Electrodynamics (see the section Excited State Dynamics), using a path integral approach to the dynamics, as described in our recent papers [598, 599]. The computation of these rates relies on the harmonic approximation for the nuclear normal modes. Provided this approximation holds, the results closely match experimental data.

The theory can do most of what ORCA_ASA can and more, such as including vibronic coupling in forbidden transitions (the so-called Herzberg-Teller effect, HT), considering Duschinsky rotations between modes of different states, solving the equations using different coordinate systems, etc. There are also seven new approaches to obtain the excited state geometry and Hessian without necessarily optimizing its geometry. Many keywords and options are available, but most of the defaults already give good results. Let’s get into specific examples, starting with the absorption spectrum. Please refer to section Excited State Dynamics for a complete keyword list and details.

5.5.1. Absorption Spectrum

5.5.1.1. The ideal model, Adiabatic Hessian (AH)

To predict absorption or emission rates, including all vibronic transitions, ideally, one requires both the ground state (GS) and excited state (ES) geometries and Hessians. For instance, when predicting the absorption spectrum for benzene, which exhibits one band above 220 nm corresponding to a symmetry-forbidden excitation to the S1 state, the process is straightforward. Ground state information can be obtained from (Sec. Geometry Optimizations):

!B3LYP DEF2-SVP OPT FREQ
* XYZFILE 0 1 BEN.xyz

and the S1 ES from (Sec. Excited State Geometry Optimization):

!B3LYP DEF2-SVP OPT FREQ
%TDDFT
  NROOTS   5
  IROOT    1
END
* XYZFILE 0 1 BEN_S1.xyz

Assuming DFT/TD-DFT here, but other methods can also be used (see Tips, Tricks and Troubleshooting). With both Hessians available, the ESD module can be accessed from:

!B3LYP DEF2-SVP TIGHTSCF ESD(ABS)
%TDDFT
  NROOTS     5
  IROOT      1
END
%ESD
  GSHESSIAN  "BEN.hess"
  ESHESSIAN  "BEN_S1.hess"
  DOHT       TRUE
END
* XYZFILE 0 1 BEN.xyz

Important

The geometry must match that in the GS Hessian when calling the ESD module. You can obtain it from the .xyz file after geometry optimization or directly copy it from the .hess file (remember to use BOHRS on the input to correct the units, if obtained from the .hess).

You must provide both names for the Hessians and set DOHT to TRUE here because the first transition of benzene is symmetry forbidden, with an oscillator strength of 2e-6. Therefore, all intensity arises from vibronic coupling (HT effect) [598]. In molecules with strongly allowed transitions, this parameter can typically remain FALSE (the default). Some calculation details are printed, including the computation of transition dipole derivatives for the HT component, and the spectrum is saved as BASENAME.spectrum.

Energy                  TotalSpectrum           IntensityFC             IntensityHT
10807.078728            2.545915e-02            2.067393e-07            2.545894e-02
10828.022679            2.550974e-02            2.071508e-07            2.550954e-02
10848.966630            2.556034e-02            2.075624e-07            2.556013e-02
...

The first column has the total spectrum, but the contributions from the Franck-Condon part and the Herzberg-Teller part are also discriminated. As you can see, the FC intensity is less than 1% of the HT intensity here, highlighting the importance of including the HT effect. It is important to note that, in theory, the absorbance intensity values correspond to the experimental \(\varepsilon\) (in L mol cm\(^{-1}\)), and they depend on the spectral lineshape. The TotalSpectrum column can be plotted using any software to obtain the spectrum named Full AH spectrum (shown in blue), in Fig. 5.4 below.

Fig. 5.4 Here is the experimental absorption spectrum for benzene (shown in black on the left), alongside predictions made using ORCA_ESD at various PES approximations.

The spectrum obtained is very close to the experimental results at 298K, even when simply using all the defaults, and it could be further improved by adjusting parameters such as lineshape, as discussed in detail in Sec. Fluorescence Rates and Spectrum and Sec. Excited State Dynamics.

Note

• The path integral approach in ORCA_ESD is much faster than the more traditional approach of calculating all vibronic transitions with non-negligible intensities, one by one [600]. This is especially true for large systems, where the number of bright vibronic transitions may potentially scale exponentially, but our approach’s scaling remains polynomial (in fact near linear scaling in favorable cases [598]). The price to pay is that one can no longer read off the compositions of the vibronic states from the spectrum, in other words, one cannot assign the peaks without doing further calculations. However, one can know whether a given vibrational mode contributes to a given peak, by repeating the ESD calculation with a few modes removed, and see if the peak is still present. This can be conveniently done using the MODELIST or SINGLEMODE keywords. More information can be found in Sec. Excited State Dynamics.

• The Huang-Rhys factors are important tools for qualitative and quantitative analysis of the contributions of each vibrational mode to the vibrationally resolved spectrum (and also to the transition rate constants, as will be discussed later). They can be requested by setting PRINTLEVEL in the %ESD module to 3 or above.

Of course, it is not always possible to obtain the excited state (ES) geometry due to root flipping, or it might be too costly for larger systems. Therefore, some approximations to the ES Potential Energy Surface (PES) have been developed.

5.5.1.2. The simplest model, Vertical Gradient (VG)

The minimal approximation, known as Vertical Gradient (VG), assumes that the excited state (ES) Hessian equals the ground state (GS) Hessian and extrapolates the ES geometry from the ES gradient and that Hessian using some step (Quasi-Newton or Augmented Hessian, which is the default here). Additionally, in this scenario, the simplest Displaced Oscillator (DO) model is employed, ensuring fast computation [598]. To use this level of approximation, simply provide an input like:

!B3LYP DEF2-SVP TIGHTSCF ESD(ABS)
%TDDFT
  NROOTS     5
  IROOT      1
END
%ESD
  GSHESSIAN  "BEN.hess"
  DOHT       TRUE
  HESSFLAG   VG    #DEFAULT
END
* XYZFILE 0 1 BEN.xyz

OBS: If no GSHESSIAN is given, it will automatically look for an BASENAME.hess file.

Choosing one of the methods in ORCA to compute excited state information is essential. Here, we utilize TD(A)-DFT with IROOT 1 to compute properties for the first excited state. TD(A)-DFT is currently the sole method offering analytic gradients for excited states; selecting any other method will automatically enforce NUMGRAD.

Important

Please note that certain methods, such as STEOM-DLPNO-CCSD, require significant time to compute numerical gradients. In such cases, we recommend using DFT/TD-DFT Hessians and employing the higher-level method solely for single points.

If everything is set correctly, after the regular single point calculation, the ESD module in ORCA will initiate. It proceeds to obtain the excited state (ES) geometry, compute derivatives, and predict the spectrum. The resulting normalized spectrum can be observed in Fig. 5.4, depicted in red. Due to such simple model, the spectrum is also simplified. While this simplicity is less critical for larger molecules, it highlight the potential benefit of employing an intermediate model.

5.5.1.3. A better model, Adiabatic Hessian After a Step (AHAS)

A reasonable compromise between a full geometry optimization and a simple step with the same Hessian is to perform a step and then recalculate the ES Hessian at that geometry. This approach is referred to here as Adiabatic Hessian After Step (AHAS). In our tests, it can be invoked with the following input:

!B3LYP DEF2-SVP TIGHTSCF ESD(ABS)
%TDDFT
  NROOTS     5
  IROOT      1
END
%ESD
  GSHESSIAN  "BEN.hess"
  DOHT       TRUE
  HESSFLAG   AHAS
END
* XYZFILE 0 1 BEN.xyz

The spectrum obtained corresponds to the green line in Fig. 5.4. As shown, it closely resembles the spectrum obtained using AH, where a full geometry optimization was performed. Although not set as the default, this method comes highly recommended based on our experience [598]. Another advantage of this approach is that the derivatives of the transition dipole are computed simultaneously over Cartesian displacements on the ES structure using the numerical Hessian. Subsequently, these modes are straightforwardly converted.

OBS: The transition dipoles used in our formulation are always those of the FINAL state geometry. For absorption, this corresponds to the ES, so in AHAS, the derivatives are computed over this geometry. For fluorescence, the default behavior is to recompute the derivatives over the GS geometry. Alternatively, you can choose to save time and convert directly from ES to GS by setting CONVDER TRUE (though this is an approximation). For more details, refer to Sec. Excited State Dynamics.

5.5.1.4. Other PES options

There are also a few other options that can be set using HESSFLAG. For example, you can calculate the vertical ES Hessian over the GS geometry and perform a step, known as the Vertical Hessian (HESSFLAG VH) method. This method has the advantage that the geometry step is expected to be better because it does not assume the initial ES Hessian is equal to the GS Hessian. However, it is likely to encounter negative frequencies on that VH, since you are not at the ES minimum. By default, ORCA will turn negative frequencies into positive ones, issuing a warning if any were lower than -300 cm\(^{-1}\). You can also choose to completely remove them (and the corresponding frequencies from the GS) by setting IFREQFLAG to REMOVE or leave them as negative with IFREQFLAG set to LEAVE under %ESD. Just be aware that an odd number of negative frequencies might disrupt the calculation of the correlation function, so be sure to check.

If your excited state is localized and you prefer not to recalculate the entire Hessian, you can opt for a Hybrid Hessian (HH) approach. This involves recomputing the ES Hessian only for specific atoms listed in HYBRID_HESS under %FREQ (Vibrational Frequencies). The HH method uses the GS Hessian as a base but adjusts it at the specified atoms. This computation can be performed either before or after the step, offering two variations: Hybrid Hessian Before Step (HESSFLAG HHBS) or Hybrid Hessian After Step (HESSFLAG HHAS). When using either of these options, derivatives are recalculated across the modes as needed.

Another approach involves comparing the ES Hessian with the GS Hessian and selectively recomputing frequencies that differs. This method works by applying a displacement based on the GS Hessian and evaluating the resulting energy change. If the predicted mode matches the actual mode, the prediction should be accurate. However, if the difference exceeds a specified threshold, the gradient is computed, and the frequency for that mode is recalculated accordingly. The final ES Hessian is then derived from the Updated Frequencies (UF) and the original GS Hessian.

This approach offers the advantage of minimizing the computation of ES gradients typical in standard ES Hessians, thereby speeding up the process. By default, the system checks for frequency errors of approximately 20%. You can adjust this threshold using the UPDATEFREQERR flag; for instance, setting UPDATEFREQERR to 0.5 under %ESD allows for a larger error tolerance of 50%. Additionally, you can implement either the Updated Frequencies Before Step (HESSFLAG UFBS) or the Updated Frequencies After Step (UFAS) methods. Transition dipole derivatives are computed concurrently with the update process.

OBS: All these options apply to Fluorescence and resonant Raman as well.

5.5.1.5. Duschinsky rotations

The ES modes can sometimes be expressed as linear combinations of the GS modes (see Sec. General Aspects of the Theory), a phenomenon known in the literature as Duschinsky rotation [601]. In our formulation within ORCA_ESD, it is possible to account for this effect, which reflects a closer approximation to real-world scenarios, albeit at a higher computational cost.

You can enable this feature by setting USEJ TRUE; otherwise, the rotation matrix J defaults to unity. For instance, in the case of benzene, while the effect may not be pronounced, there is noticeable improvement in matching peak ratios with experimental data when incorporating rotations. Exploring this option may reveal more significant impacts in other cases.

Fig. 5.5 Experimental absorption spectrum for benzene (black on the left) and the effect of Duschinsky rotation on the spectrum.

5.5.1.6. Temperature effects

In our model, the effects of the Boltzmann distribution due to temperature are exactly accounted for [598]. The default temperature is set to 298.15 K, but you can specify any other temperature by adjusting the TEMP parameter under %ESD. However, it is important to note that when approaching temperatures close to 0 K, numerical issues may arise. For instance, if you encounter difficulties modeling a spectrum at 5 K or wish to predict a jet-cooled spectrum, setting TEMP to 0 will activate a set of equations specifically tailored for T=0 K conditions.

As can be seen in Fig. 5.6, at 0 K there are no hot bands and fewer peaks, while at 600 K there are many more possible transitions due to the population distribution over the GS.

Fig. 5.6 Predicted absorption spectrum for benzene at different temperatures.

5.5.1.7. Multistate Spectrum

If you want to predict a spectrum that includes many different states, you should ignore the IROOT flag in all modules and instead use the STATES flag under %ESD. For example, to predict the absorption spectra of pyrene in the gas phase and consider the first twenty states, you would specify:

!B3LYP DEF2-TZVP(-F) TIGHTSCF ESD(ABS)
%TDDFT
  NROOTS     20
END
%ESD
  GSHESSIAN  "PYR.hess"
  ESHESSIAN  "PYR_S1.hess"
  DOHT       TRUE
  STATES     1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20
  UNIT       NM
END
* XYZFILE 0 1 PYR.xyz

This input would result in the spectra shown in Fig. 5.7. In this case, each individual spectrum for every state will be saved as BASENAME.spectrum.root1, BASENAME.spectrum.root2, etc., while the combined spectrum, which is the sum of all individual spectra, will be saved as BASENAME.spectrum.

Fig. 5.7 Predicted absorption spectrum for pyrene in gas phase (solid blue) in comparison to the experiment (dashed grey) at 298 K.

OBS: The flag UNIT can be used to control the output unit of the X axis. Its values can be CM-1, NM or EV and it only affects the OUTPUT, the INPUT should always be in cm\(^{-1}\)

5.5.2. Fluorescence Rates and Spectrum

5.5.2.1. General Aspects

The prediction of fluorescence rates and spectra can be performed in a manner analogous to absorption, as described above, by using ESD(FLUOR) on the main input line. You can select any of the methods described earlier to obtain the Potential Energy Surface (PES) by setting the appropriate HESSFLAG. The primary distinction is that the transition dipoles must correspond to the geometry of the ground state (GS), while all other aspects remain largely unchanged.

Fig. 5.8 Predicted absorption (right) and emission (left) spectrum for benzene in hexane at 298.15 K.

As depicted in Fig. 5.8, the fluorescence spectrum also closely matches the experimental data [598]. The difference observed in the absorption spectrum in Fig. 5.8, compared to previous spectra, arises because the experiment was conducted in a solvent environment. Therefore, we adjusted the linewidth to align with the experimental data.

OBS: It is common for the experimental lineshape to vary depending on the setup, and this can be adjusted using the LINEW flag (in cm\(^{-1}\)). There are four options for the lineshape function controlled by the LINES flag: DELTA (for a Dirac delta function), LORENTZ (default), GAUSS (for a Gaussian function), and VOIGT (a Voigt profile, which is a product of Gaussian and Lorentzian functions).

OBS2: The DELE and TDIP keywords can be used to input adiabatic (not vertical!) excitation energy and transition dipole moment computed at a higher level of theory. This enables calculating the computationally intensive Hessians (especially the excited state Hessian) at a low level of theory without compromising the accuracy. For more details, see Sec. Mixing methods.

If you need to control the lineshapes separately for Gaussian (GAUSS) and Lorentzian (LORENTZ), you can set LINEW for Lorentzian and INLINEW for Gaussian (where “I” stands for Inhomogeneous Line Width).

!B3LYP DEF2-SVP TIGHTSCF ESD(FLUOR)
%TDDFT
  NROOTS     5
  IROOT      1
END
%ESD
  GSHESSIAN  "BEN.hess"
  ESHESSIAN  "BEN_S1.hess"
  DOHT       TRUE
  LINES      VOIGT
  LINEW      75
  INLINEW    200
END
* XYZFILE 0 1 BEN.xyz

OBS: The LINEW and INLINEW are NOT the full width half maximum (\(FWHM\)) of these curves. However, they are related to them by: \(FWHM_{lorentz} = 2 \times LINEW\); \(FWHM_{gauss} = 2.355 \times INLINEW\).

For the VOIGT curve, it is a little more complicated but in terms of the other FWHMs, it can be approximated as: \(FWHM_{voigt} = 0.5346 \times FWHM_{lorentz} + \sqrt{(0.2166 \times FWHM_{lorentz}^2 + FWHM_{gauss}^2) }\).

5.5.2.2. Rates and Examples

When you select ESD(FLUOR) on the main input, the fluorescence rate will be printed at the end of the output, with contributions from Franck-Condon (FC) and Herzberg-Teller (HT) mechanisms discriminated. If you use CPCM, the rate will be multiplied by the square of the refractive index, following Strickler and Berg [602].

If you calculate a rate without CPCM but still want to account for the solvent effect, remember to multiply the final rate by this factor. Below is an excerpt from the output of a calculation with CPCM (hexane):

Warning

Whenever using ESD with CIS/TD-DFT and solvation, CPCMEQ will be set to TRUE by default, since the excited state should be under equilibrium conditions! More info in Including solvation effects via LR-CPCM theory.

...
          ***Everything is set, now computing the correlation function***

Homogeneous linewidht is:			50.00 cm-1
Number of points:				131072
Maximum time:					1592.65 fs
Spectral resolution:				3.33 cm-1
Temperature used:				298.15 K
Z value:					5.099843e-42
Energy difference:				41049.37 cm-1
Reference transition dipole (x,y,z):		(0.00004 0.00000),
                                    		(0.00002 0.00000),
                                    		(-0.00058 0.00000) 
Calculating correlation function:		...done
Last element of the correlation function:	0.000000,-0.000000
Computing the Fourier Transform:		...done

The calculated fluorescence rate constant is	1.688355e+06 s-1*
with 0.00% from FC and 100.00% from HT

*The rate is multiplied by the square of the refractive index

The fluorescence spectrum was saved in		BASENAME.spectrum

In one of our theory papers, we investigated the calculation of fluorescence rates for the set of molecules presented in Fig. 5.9. The results are summarized in Fig. 5.10 for some of the methods used to obtain the Potential Energy Surface (PES) mentioned.

Fig. 5.9 The set of molecules studied, with rates on Fig. 5.10.

Fig. 5.10 Predicted emission rates for various molecules in hexane at 298.15 K. The numbers below the labels are the HT contribution to the rates.

5.5.3. Phosphorescence Rates and Spectrum

5.5.3.1. General Aspects

As with fluorescence, phosphorescence rates and spectra can be calculated if spin-orbit coupling is included in the excited state module (please refer to the relevant publication [599]). To enable this, ESD(PHOSP) must be selected in the main input, and both a GSHESSIAN and a TSHESSIAN must be provided. The triplet Hessian can be computed analytically from the spin-adapted triplets.

!B3LYP DEF2-TZVP(-F) CPCM(ETHANOL) OPT FREQ
%TDDFT
  NROOTS 5
  IROOTMULT TRIPLET
END
* XYZ 0 1 
C         -0.82240       -0.05739        0.00515
C          0.42295        0.77803        0.02146
H         -0.85252       -0.69527        0.89195
H         -0.85090       -0.66429       -0.90325
H         -1.69889        0.59680        0.01431
C          1.74379        0.02561       -0.01818
C          2.98907        0.86121       -0.00686
H          3.01366        1.50199       -0.89176
H          3.86561        0.20724       -0.02398
H          3.02300        1.46514        0.90332
O          0.42398        2.00161        0.06749
O          1.74282       -1.19814       -0.05965
*

or, in this case, by computing the ground state triplet by simply setting the multiplicity to three:

!B3LYP DEF2-TZVP(-F) CPCM(ETHANOL) OPT FREQ
* XYZFILE 0 3 BIA.xyz

Alternatively, one can use methods like VG, AHAS, etc., to approximate the triplet geometry and Hessian. However, this approach requires preparing the Hessian in a separate ESD run (Sec. Approximations to the excited state PES).

Additionally, you must input the adiabatic energy difference between the ground singlet and ground triplet states at their respective geometries (without any zero-point energy correction) using the DELE flag under %ESD. In this case, the spin-adapted triplet computed previously serves as our reference triplet state. An example input for the rate calculation using TDDFT is as follows:

!B3LYP DEF2-TZVP(-F) TIGHTSCF CPCM(ETHANOL) ESD(PHOSP) RI-SOMF(1X)
%TDDFT
  NROOTS  20
  DOSOC   TRUE
  TDA     FALSE
  IROOT   1
END
%ESD    GSHESSIAN       "BIA.hess"
        TSHESSIAN       "BIA_T1.hess"
        DOHT            TRUE
        DELE            17260
END
* XYZFILE 0 1 BIA.xyz

$NEW_JOB

!B3LYP DEF2-TZVP(-F) TIGHTSCF CPCM(ETHANOL) ESD(PHOSP) RI-SOMF(1X)
%TDDFT
  NROOTS  20
  DOSOC   TRUE
  TDA     FALSE
  IROOT   2
END
%ESD    GSHESSIAN       "BIA.hess"
        TSHESSIAN       "BIA_T1.hess"
        DOHT            TRUE
        DELE            17260
END
* XYZFILE 0 1 BIA.xyz

$NEW_JOB

!B3LYP DEF2-TZVP(-F) TIGHTSCF CPCM(ETHANOL) ESD(PHOSP) RI-SOMF(1X)
%TDDFT
  NROOTS  20
  DOSOC   TRUE
  TDA     FALSE
  IROOT   3
END
%ESD    GSHESSIAN       "BIA.hess"
        TSHESSIAN       "BIA_T1.hess"
        DOHT            TRUE
        DELE            17260
END
* XYZFILE 0 1 BIA.xyz

Phosphorescence rate calculation are always accompanied by the generation of the vibrationally resolved phosphorescence spectrum, which can be visualized in the same way as fluorescence spectra.

OBS.: When computing phosphorescence rates, each rate from individual spin sub-levels must be requested separately. You may use the $NEW_JOB option, just changing the IROOT, to write everything in a single input. After SOC, the three triplet states (\(T_1\) with \(M_S\) = -1, 0 and +1) will split into IROOTs 1, 2 and 3, and all of them must be included when computing the final phosphorescence rate. In this case, it is reasonable to assume that the geometries and Hessians of these spin sub-levels are the same, and we will use the same .hess file for all three.

OBS2.: The ground state geometry should be used in the input file, similar to the case of fluorescence (vide supra).

OBS3.: Apart from DELE, one can also use the TDIP keyword to input a high-level transition dipole moment, similar to the fluorescence case. This enables e.g. the calculation of phosphorescence rates/spectra using e.g. NEVPT2 or DLPNO-STEOM-CCSD transition dipole moments, with (TD)DFT geometries and Hessians. Note however that the transition dipole moment in phosphorescence processes is complex, so 6 instead of 3 components are required.

Here, we are computing the rate and spectrum for biacetyl in ethanol at 298 K. The geometries and Hessians were obtained as previously described, with the ground triplet computed from a simple open-shell calculation. To compute the rate, the flag DOSOC must be set to TRUE under %TDDFT (Sec Spin-orbit coupling), or the respective module, and it is advisable to set a large number of roots to ensure a good mixing of states.

Please note that we have chosen the RI-SOMF(1X) option for the spin-orbit coupling integrals, but any of the available methods can be used (Sec. The Spin-Orbit Coupling Operator).

5.5.3.2. Calculation of rates

As you can see, the predicted spectra for biacetyl (Fig. 5.11) are quite close to the experimental results [599, 603]. The calculation of the phosphorescence rate is more complex because there are three triplet states that contribute. Therefore, the observed rate must be taken as an average of these three states.

\[k^{phosp}_{av} = \frac{ k_1 + k_2 + k_3}{ 3}\]

To be even more strict and account for the Boltzmann population distribution at a given temperature \(T\) caused by the Zero Field Splitting (ZFS), one should use [604]:

(5.28)\[ k^{phosp}_{av} = \frac{ k_1 + k_2e^{-(\Delta E_{1,2}/k_B T) } + k_3e^{-(\Delta E_{1,3}/k_B T) }}{1 + e^{-(\Delta E_{1,2}/k_B T) } +e^{-(\Delta E_{1,3}/k_B T) } } \]

where \(\Delta E_{1,2}\) is the energy difference between the first and second states, and so on.

After completion of each calculation, the rates for the three triplets were 8.91 s\(^{-1}\), 0.55 s\(^{-1}\), and 284 s\(^{-1}\). Using (5.28), the final calculated rate is about 98 s\(^{-1}\), while the best experimental value is 102 s\(^{-1}\) (at 77K) [605], with about 40% deriving from the HT effect.

Fig. 5.11 The experimental (dashed red) and theoretical (solid black, displaced by about 2800 cm\(^{-1}\)) phosphorescence spectra for biacetyl, in ethanol at 298 K.

OBS: A subtlety arises when the final state is not a singlet state, for example in radical phosphorescence (doublet ground state) or singlet oxygen phosphorescence (triplet ground state). In this case the most rigorous treatment would be to sum over the final states but average over the initial states. For example, with quartet-to-doublet phosphorescence one gets

(5.29)\[\begin{split} k^{phosp}_{av} = \frac{ k_{1\to 1} + k_{2\to 1}e^{-(\Delta E_{1,2}/k_B T) } + k_{3\to 1}e^{-(\Delta E_{1,3}/k_B T) } + k_{4\to 1}e^{-(\Delta E_{1,4}/k_B T) }}{1 + e^{-(\Delta E_{1,2}/k_B T) } +e^{-(\Delta E_{1,3}/k_B T) } + e^{-(\Delta E_{1,4}/k_B T) } } \nonumber\\ + \frac{ k_{1\to 2} + k_{2\to 2}e^{-(\Delta E_{1,2}/k_B T) } + k_{3\to 2}e^{-(\Delta E_{1,3}/k_B T) } + k_{4\to 2}e^{-(\Delta E_{1,4}/k_B T) }}{1 + e^{-(\Delta E_{1,2}/k_B T) } +e^{-(\Delta E_{1,3}/k_B T) } + e^{-(\Delta E_{1,4}/k_B T) } } \end{split}\]

where \(k_{2\to 1}\) is the phosphorescence rate constant from the second sublevel of the initial quartet to the first sublevel of the final doublet, etc. Note that the Boltzmann factors of the final state do not enter the expression. Unfortunately, since U-TDDFT is spin contaminated and unsuitable for calculating SOC-corrected transition dipole moments, the transition dipoles in this case have to be calculated by more advanced methods, such as DFT/ROCIS or multireference methods. The transition dipole should then be given in the input file using the TDIP keyword.

5.5.4. Intersystem Crossing Rates (unpublished)

5.5.4.1. General Aspects

Yet another application of the path integral approach is to compute intersystem crossing rates, or non-radiative transition rates between states of different multiplicities. This can be calculated if one has two geometries, two Hessians, and the relevant spin-orbit coupling matrix elements.

The input is similar to those discussed above. Here ESD(ISC) should be used on the main input to indicate an InterSystem Crossing calculation, and the Hessians should be provided by ISCISHESSIAN and ISCFSHESSIAN for the initial and final states, respectively. Please note that the geometry used in the input file should correspond to that of the FINAL state, specified through the ISCFSHESSIAN flag. The relevant matrix elements can be computed using any method available in ORCA and inputted as SOCME Re,Im under %ESD where Re and Im represent its real and imaginary parts (in atomic units!).

As a simple example, one could compute the excited singlet and ground triplet geometries and Hessians for anthracene using TD-DFT. Then, compute the spin-orbit coupling (SOC) matrix elements for a specific triplet spin-sublevel using the same method (see the details below), potentially employing methods like CASSCF, MRCI, STEOM-CCSD, or another theoretical level. Finally, obtain the intersystem crossing (ISC) rates using an input such as:

!ESD(ISC) NOITER
%ESD
  ISCISHESSIAN  "ANT_S1.hess"
  ISCFSHESSIAN  "ANT_T1.hess"
  DELE          11548
  SOCME         0.0, 2.33e-5
END
* XYZFILE 0 1 ANT_T1.xyz

The SOCMEs between a singlet state and a triplet state consist of three complex numbers, not just one, because the triplet state has three sublevels. If the user uses the SOCME of one of the sublevels as input to the ISC rate calculation, this gives the ISC rate associated with that particular sublevel. However, experimentally one usually does not distinguish the three sublevels of a triplet state, and experimentally ISC rates are reported as if the three sublevels of a triplet state are the same species. Therefore, the rate of singlet-to-triplet ISC is the sum of the ISC rates from the singlet state to the three triplet sublevels. Fortunately, in case the Herzberg-Teller effect (vide infra) can be neglected, it is not necessary to perform three rate calculations and add up the rates, since the rate is proportional to the squared modulus of the SOCME. Thus, one can run a single ESD calculation where the SOCME is the square root of the summed squared moduli of the three SOCME components.

As an illustration, consider the \(S_1\) to \(T_1\) ISC rate of acetophenone. First, we optimize the \(S_0\) geometry, and (after manually tweaking the geometry to break mirror symmetry) use it as an initial guess for the geometry optimization and frequency calculations of the \(S_1\) and \(T_1\) states. Then, we calculate the \(S_1\)-\(T_1\) SOCMEs at the \(T_1\) geometry (note that, as usual, final state geometries should be used for ESD calculations; this may differ from some programs other than ORCA). These calculations are conveniently done using a compound script, although the individual steps can of course also be done using separate input files.

%pal nprocs 16 end

* xyz 0 1
  C      1.512698    7.783764   -0.013405
  C      2.900029    7.735359   -0.016012
  C      3.664170    8.950745    0.000408
  C      2.952045   10.199539    0.007630
  C      1.564497   10.214795    0.009890
  C      0.827311    9.015246    0.000726
  H      0.946857    6.847253   -0.027731
  H      3.394565    6.763402   -0.041976
  H      3.505090   11.140193    0.017889
  H      1.039592   11.175094    0.019479
  H     -0.265468    9.038211    0.000969
  C      5.059695    8.958412    0.000442
  O      5.733735   10.161120   -0.048672
  C      5.927824    7.713913    0.020029
  H      5.442615    6.938582    0.639989
  H      6.073177    7.326421   -1.014490
  H      6.923426    7.950459    0.447785
 *

%compound

new_step # Compound 1: S1 opt
! B3LYP def2-SV(P) opt tightopt freq

%tddft
tda false
nroots 2
iroot 1
end

step_end

new_step # Compound 2: T1 opt
! B3LYP def2-SV(P) opt tightopt freq

* xyz 0 3
  C      1.512698    7.783764   -0.013405
  C      2.900029    7.735359   -0.016012
  C      3.664170    8.950745    0.000408
  C      2.952045   10.199539    0.007630
  C      1.564497   10.214795    0.009890
  C      0.827311    9.015246    0.000726
  H      0.946857    6.847253   -0.027731
  H      3.394565    6.763402   -0.041976
  H      3.505090   11.140193    0.017889
  H      1.039592   11.175094    0.019479
  H     -0.265468    9.038211    0.000969
  C      5.059695    8.958412    0.000442
  O      5.733735   10.161120   -0.048672
  C      5.927824    7.713913    0.020029
  H      5.442615    6.938582    0.639989
  H      6.073177    7.326421   -1.014490
  H      6.923426    7.950459    0.447785
 *

step_end

new_step # Compound 3: SOC at T1 geometry
! B3LYP def2-SV(P)

%tddft
tda false
nroots 3
triplets true
dosoc true
end

# Here it is assumed that the input file is named "a.inp"
* xyzfile 0 1 a_Compound_2.xyz

step_end
end

After verifying that neither of the Hessians have imaginary frequencies (which is very important!), we can read the computed SOCMEs:

      --------------------------------------------------------------------------------
                      CALCULATED SOCME BETWEEN TRIPLETS AND SINGLETS
      --------------------------------------------------------------------------------
           Root                          <T|HSO|S>  (Re, Im) cm-1
         T      S             Z                     X                     Y
      --------------------------------------------------------------------------------
         1      0    (   0.00 ,   -2.00 )    (   0.00 ,   29.24 )    (  -0.00 ,  -41.11 )
         1      1    (   0.00 ,   -0.59 )    (   0.00 ,    1.79 )    (  -0.00 ,   -2.57 )
         1      2    (   0.00 ,    0.52 )    (   0.00 ,   -3.19 )    (  -0.00 ,    3.21 )
         1      3    (   0.00 ,   -2.39 )    (   0.00 ,   14.57 )    (  -0.00 ,  -19.53 )
         2      0    (   0.00 ,   -0.11 )    (   0.00 ,    2.78 )    (  -0.00 ,   -2.72 )
         2      1    (   0.00 ,    2.25 )    (   0.00 ,  -20.07 )    (  -0.00 ,   28.07 )
         2      2    (   0.00 ,    0.02 )    (   0.00 ,   -0.13 )    (  -0.00 ,    0.29 )
         2      3    (   0.00 ,   -0.17 )    (   0.00 ,    0.59 )    (  -0.00 ,   -1.27 )
         3      0    (   0.00 ,   -0.01 )    (   0.00 ,    0.05 )    (  -0.00 ,   -0.06 )
         3      1    (   0.00 ,   -0.01 )    (   0.00 ,    0.19 )    (  -0.00 ,   -1.36 )
         3      2    (   0.00 ,   -0.01 )    (   0.00 ,   -0.05 )    (  -0.00 ,   -0.14 )
         3      3    (   0.00 ,   -0.00 )    (   0.00 ,    0.14 )    (  -0.00 ,   -0.16 )

The “total” SOCME between \(S_1\) and \(T_1\) is then calculated, from the line that begins with “1 1”, as

\[ \sqrt{0.00^2 + (-0.59)^2 + 0.00^2 + 1.79^2 + 0.00^2 + 2.57^2} cm^{-1} = 3.19 cm^{-1} = 1.45\times 10^{-5} au \]

One should therefore write socme 1.45e-5 in the %esd block in the subsequent ISC rate calculation.

Importantly, the above approach is only applicable to singlet-to-triplet ISC, but not to triplet-to-singlet ISC (including, but not limited to, \(T_1\to S_0\) and \(T_1\to S_1\) processes). In the latter case, assuming that the triplet sublevels are degenerate and in rapid equilibrium, we obtain that the observed rate constant is the average, not the sum, of the rate constants of the three triplet sublevels, because each triplet sublevel has a Boltzmann weight of 1/3. Therefore, the “effective” SOCME that should be plugged into the ESD module to get the observed rate constant is (here the squared modulus \(|SOCME_x|^2\) should be calculated as \(Re(SOCME_x)^2 + Im(SOCME_x)^2\), etc.)

(5.30)\[ SOCME_{av} = \sqrt{\frac{|SOCME_x|^2 + |SOCME_y|^2 + |SOCME_z|^2}{3}} \]

i.e. a factor of \(\sqrt{3}\) smaller than the singlet-to-triplet case. However, both of the two assumptions (degenerate triplet sublevels, and rapid equilibrium between sublevels) may fail under certain circumstances, which may contribute to the error of the predicted rate. Nevertheless, in many cases the present, simple approach still provides a rate with at least the correct order of magnitude.

OBS.: The adiabatic energy difference is NOT computed automatically for ESD(ISC), so you must provide it in the input. This is the energy of the initial state minus the energy of the final state, each evaluated at its respective geometry.

OBS2.: All the other options concerning changes of coordinate system, Duschinsky rotation, etc., are also available here.

OBS3.: For many molecules, the \(S_1 \to T_1\) ISC process is not the dominant ISC pathway. This is because the excited state compositions of \(S_1\) and \(T_1\) are often similar, and therefore ISC transitions between them frequently do not satisfy the El-Sayed rule. Even if the only experimentally observed excited states are \(S_1\) and \(T_1\), it may still be that the initial ISC is dominated by \(S_1 \to T_n (n>1)\), followed by ultrafast \(T_n \to T_1\) internal conversion.

OBS4.: Similarly, if the molecule starts at a high singlet state \(S_n (n>1)\), the dominant ISC pathway is not necessarily the direct ISC from \(S_n\) to one of the triplet states. Rather, it is possible (but not necessarily true) that \(S_n\) first decays to a lower singlet excited state before the ISC occurs.

OBS5.: If you calculate the DELE or SOCMEs at a higher level of theory and use it as an input for the ESD calculation, please make sure that you have chosen the same excited state (in terms of state composition, not energy ordering) in the Hessian and DELE/SOCME calculations. For example, suppose that you have obtained the geometry and Hessian of the \(T_2\) state, but the \(T_2\) state of the higher level of theory has a very different state composition than the \(T_2\) state at the level of theory used in the Hessian calculation; rather, it is \(T_3\) at the high level of theory that shares the same composition as the \(T_2\) state at the lower level of theory. In this case, you should use the SOCME related to \(T_3\) in the SOCME output file.

OBS6.: The ESD module does not require that the final state of the ISC process is energetically lower than the initial state. Therefore, reverse ISC (RISC) rates can be calculated in exactly the same way as ISC rates. Note however that (1) if you want to supply the adiabatic energy difference using the DELE keyword, the energy difference should be negative; and (2) whether one should sum or average the three components of the SOCMEs depend on whether the final state is a triplet state, not whether the lower state is a triplet state.

OBS7.: ISC transitions between states other than singlets and triplets (for example between a doublet state an a quartet state) can also be calculated, provided that the SOCMEs are calculated by a properly spin-adapted or multireference method, such as DFT/ROCIS or NEVPT2. The squared moduli of the sublevels’ SOCMEs should be summed over all final state spin sublevels but averaged over all initial state spin sublevels, similar to the phosphorescence case (Calculation of rates).

5.5.4.2. ISC, TD-DFT and the HT effect

In the anthracene example above, the result is an ISC rate (\(k_{ISC}\)) smaller than \(1 s^{-1}\), which is quite different from the experimental value of \(10^{8} s^{-1}\) at \(77 K\) [605]. The reason for this discrepancy, in this particular case, is because the ISC occurs primarily due to the Herzberg-Teller effect, which must also be included. To achieve this, one needs to compute the derivatives of the SOCMEs over the normal modes, currently feasible only using CIS/TD-DFT.

When using the %CIS/TDDFT option, you can control the SROOT and TROOT flags to select the singlet and triplet states for which SOCMEs are computed, and the TROOTSSL flag to specify the triplet spin-sublevel (1, 0, or -1).

In practice, to obtain an ISC rate (\(k_{ISC}\)) close enough to experimental values, one would need to consider all possible transitions between the initial singlet and all available final states. For anthracene, these are predicted to be the ground triplet (\(T_1\)) and the first excited triplet (\(T_2\)), consistent with experimental observations [606], while the next triplet (\(T_3\)) is energetically too high to be significant (Fig. 5.12 below). An example input used to calculate the \(k_{ISC}\) from \(S_1\) to \(T_1\) at \(77K\) is:

!B3LYP DEF2-TZVP(-F) TIGHTSCF ESD(ISC)
%TDDFT  NROOTS  5
        SROOT   1
        TROOT   1
        TROOTSSL 0
        DOSOC   TRUE
END
%ESD    ISCISHESS       "ANT_S1.hess"
        ISCFSHESS       "ANT_T1.hess"
        USEJ            TRUE
        DOHT            TRUE
        TEMP            77
        DELE            11548
END
* XYZFILE 0 1 ANT_T1.xyz

$NEW_JOB

!B3LYP DEF2-TZVP(-F) TIGHTSCF ESD(ISC)
%TDDFT  NROOTS  5
        SROOT   1
        TROOT   1
        TROOTSSL -1
        DOSOC   TRUE
END
%ESD    ISCISHESS       "ANT_S1.hess"
        ISCFSHESS       "ANT_T1.hess"
        USEJ            TRUE
        DOHT            TRUE
        TEMP            77
        DELE            11548
END
* XYZFILE 0 1 ANT_T1.xyz

...

Fig. 5.12 Scheme for the calculation of the intersystem crossing in anthracene. The \(k_{ISC}(i)\) between \(S_1\) and each triplet is a sum of all transitions to the spin-sublevels and the actual observed \(k_{ISC}^{obs}\), which consolidates these transitions. On the right, there is a diagram illustrating the distribution of excited states with \(E(S_1) - E(T_n)\) depicted on the side. Since \(T_3\) is energetically too high, intersystem crossing involving \(T_3\) can be safely neglected.

Then, the derivatives of the SOCME are computed and the rates are printed at the end. By performing the same calculations for the \(T_2\) states and summing up these values, a predicted \(k_{ISC}^{obs} = 1.17 \times 10^8 s^{-1}\) can be obtained, much closer to the experimental value, which is associated with a large error anyway.

OBS.: In cases where the SOCME are relatively large, e.g., SOCME \(>5 cm^{-1}\), the Herzberg-Teller effect might be negligible, and a simple Franck-Condon calculation should yield good results. This is typically applicable to molecules with heavy atoms, where vibronic coupling is less significant.

OBS2.: Always consider that there are actually THREE triplet spin-sublevels, and transitions from the singlet to all of them should be included.

OBS3.: ISC rates are extremely sensitive to energy differences. Exercise caution when calculating them. If a more accurate excited state method is available, it should be considered for prediction.

OBS4.: The Herzberg-Teller effect is not yet implemented for ISC transitions between states that are not singlets and triplets.

5.5.5. Internal Conversion Rates (unpublished)

The ESD module can also calculate internal conversion (IC) rates from an excited state to the ground state at the TDDFT and TDA levels. Apart from the ground state and excited state Hessians, the only additional quantity that needs to be calculated is the nonadiabatic coupling matrix elements (NACMEs).

The input file is simple:

# S1-S0 IC rate of azulene
! B3LYP D3 def2-SVP ESD(IC) CPCM(methanol)

%tddft
tda false # Full TDDFT is recommended over TDA
nroots 3
iroot 1 # Change to 2 for S2-S0 IC rate, etc.
nacme true # Calculate the NACME between the iroot-th root with the ground state
etf true # Use electron translation factor (recommended)
end

%esd
gshessian "azulene_S0.hess" # Ground state Hessian (B3LYP-D3/def2-SVP)
eshessian "azulene_S1.hess" # Excited state Hessian (TD-B3LYP-D3/def2-SVP)
usej true # Use Duschinsky rotation (recommended)
end

# Ground state geometry (B3LYP-D3/def2-SVP)
* xyzfile 0 1 azulene_S0.xyz

Here the \(S_0\) geometry, as well as the \(S_0\) and \(S_1\) Hessian files, were obtained at the B3LYP-D3/def2-SVP level of theory. Note that the NACME calculation uses full TDDFT and also includes the electron-translation factor (ETF), which are the recommended practices in general. The “iroot 1” specifies that the initial state is \(S_1\); the final state is always \(S_0\) and this cannot be changed.

The computed IC rate constant is given near the end of the output file:

          ***Everything is set, now computing the correlation function***

Homogeneous linewidth is:     50.00 cm-1
Inhomogeneous linewidth is:     250.00 cm-1
Number of points:       32768
Maximum time:         157.86 fs
Temperature used:       298.15 K
Z value:          4.924300e-66
Cutoff for the correlation function:    1.00e-12
Adiabatic energy difference:      16699.89 cm-1
0-0 energy difference:        16382.09 cm-1
Calculating correlation function:   ...done
Last element of the correlation function: -0.000000,-0.000000

The calculated internal conversion rate constant is 3.823146e+08 s-1

Total run time: 0 hours 2 minutes 50 seconds

                      ****ORCA ESD FINISHED WITHOUT ERROR****

For more accurate results, one may add explicit solvation shells, since implicit solvation models only describe the electrostatic and dispersive effects of the solvent on the solute, but cannot provide the extra vibrational degrees of freedom that can help dissipating the excitation energy. Conversely, by using an implicit solvent one also misses the effect of the solvent viscosity on inhibiting the internal conversion, which is particularly important when one wants to compare against experiments conducted at low temperatures.

5.5.6. Resonant Raman Spectrum

5.5.6.1. General Aspects

Using a theoretical framework similar to what was published for Absorption and Fluorescence, we have also developed a method to compute resonant Raman spectra for molecules [607]. In this implementation, one can employ all the methods to obtain the excited state potential energy surfaces (PES) mentioned earlier using HESSFLAG, and include Duschinsky rotations and even consider the Herzberg-Teller effect on top of it. This calculation can be initiated by using ESD(RR) or ESD(RRAMAN) on the first input line. It is important to note that by default, we calculate the “Scattering Factor” or “Raman Activity,” as described by D. A. Long [608] (see Sec. Resonant Raman Spectrum for more information).

When using this module, the laser energy can be controlled by the LASERE flag. If no laser energy is specified, the 0-0 energy difference is used by default. You can select multiple energies by using LASERE 10000, 15000, 20000, etc., and if multiple energies are specified, a series of files named BASENAME.spectrum.LASERE will be saved. Additionally, it is possible to specify several states of interest using the STATES flag, but not both simultaneously.

As an example, let’s predict the resonant Raman spectrum of the phenoxyl radical. You need at least a ground state geometry and Hessian, and then you can initiate the ESD calculation using:

!PBE0 DEF2-SVP TIGHTSCF ESD(RR)
%TDDFT
  NROOTS     5
  IROOT      3
END
%ESD
  GSHESSIAN  "PHE.hess"
  LASERE     28468
END
* XYZFILE 0 2 PHE.xyz

Important

The LASERE used in the input is NOT necessarily the same as the experimental one. It should be proportional to the theoretical transition energy. For example, if the experimental 0-0 \(\Delta\)E is 30000 cm\(^{-1}\) and the laser energy used is 28000 cm\(^{-1}\), then for a theoretical \(\Delta\)E of 33000 cm\(^{-1}\), you should use a laser energy of 31000 cm\(^{-1}\) to obtain the corresponding theoretical result. At the end of the ESD output, the theoretical 0-0 \(\Delta\)E is printed for your information.

Fig. 5.13 The theoretical (solid black - vacuum and solid blue - water) and experimental (dashed red - water) resonant Raman spectrum for the phenoxyl radical.

OBS.: The actual Raman Intensity collected with any polarization at 90 degrees, the I(\(\pi/2; \parallel^{s}+\perp^{s},\perp^{i}\)) [608], can be obtained by setting RRINTES to TRUE under %ESD.

And the result is shown in Fig. 5.13. In this case, the default method VG was used. If one wants to include solvent effects, then CPCM(WATER) should be added. As can be seen, there is a noticeable difference in the main peak when calculated in water.

It is important to clarify some differences from the ORCA_ASA usage here. Using the ESD module, you do not need to select which modes you will account for in the spectra; we include all of them. Additionally, we can only operate at 0 K, and the maximum “Raman Order” is 2. This means we account for all fundamental transitions, first overtones, and combination bands, without including hot bands. This level of approximation is generally sufficient for most applications.

If you are working with a very large system and want to reduce calculation time, you can request RORDER 1 under the %ESD options. This setting includes only the fundamental transitions, omitting higher-order bands. This approach may be relevant, especially when including both Duschinsky rotations and the Herzberg-Teller effect, which can significantly increase computation time.

The rRaman spectra are printed with the contributions from “Raman Order” 1 and 2 separated as follows:

Energy			TotalSpectrum		IntensityO1		IntensityO2
0.000000		2.722264e-08		2.722264e-08		8.436299e-30
0.305176		2.824807e-08		2.824807e-08		9.043525e-30
0.610352		2.931074e-08		2.931074e-08		9.693968e-30
...

5.5.6.2. Isotopic Labeling

If you want to simulate the effect of isotopic labeling on the rRaman spectrum, there is no need to recalculate the Hessian again. Instead, you can directly modify the masses of the respective atoms in the Hessian files. This can be done by editing the $\(atoms\) section of the input file or directly in the Hessian file itself (see also Sec. Isotope Shifts). After making these adjustments, you can rerun ESD using the modified Hessian files, for example:

!PBE0 DEF2-SVP TIGHTSCF ESD(RR) CPCM(WATER)
%TDDFT
  NROOTS     5
  IROOT      3
END
%ESD
  GSHESSIAN  "PHE_WATER_ISO.hess"
  ESHESSIAN  "PHE_WATER_ISO.ES.hess"
END
* XYZFILE 0 2 PHE_WATER.xyz

As depicted in Fig. 5.14, the distinction between phenoxyl and its deuterated counterpart is evident. The peak around 1000 cm\(^{-1}\) corresponds to a C-H bond, which shifts to lower energy after deuteration. This difference of approximately 150 cm\(^{-1}\) aligns closely with experimental findings [609].

Fig. 5.14 The theoretical (solid black - C\(_6\)H\(_5\)O and solid blue - C\(_6\)D\(_5\)O) and experimental (dashed red) resonant Raman spectrum for the phenoxyl radical.

OBS: Whenever an ES Hessian is calculated using the HESSFLAG methods, it is saved in a file named BASENAME.ES.hess. If you want to repeat a calculation, you can simply use this file as an input without the need to recalculate everything.

5.5.6.3. RRaman and Linewidths

The keywords LINEW and INLINEW control the LINES function used in the calculation of the correlation function and are related to the lifetime of intermediate states and energy disordering. However, they do not determine the spectral linewidth itself, but rather the lineshape. The spectral linewidth is set independently using the RRSLINEW keyword, which defaults to 10 \(cm^{-1}\).

It’s important to note that LINEW and INLINEW significantly influence the final shape of the spectrum and should be chosen appropriately based on your specific needs. While the defaults are generally suitable, you may need to adjust them according to your requirements.

5.5.7. ESD and STEOM-CCSD or other higher level methods - the APPROXADEN option

If you plan to use the ESD module together with STEOM-CCSD, or other higher level methods such as EOM-CCSD, CASSCF/NEVPT2, some special advice must be given.

Since these methods currently do not have analytic gradients, numerical ones will be requested by default to compute the excited state geometries. This, of course, can take a significant amount of time, as they require approximately \(3 \times N_{\text{atoms}}\) single-point calculations. We strongly recommend that, in these cases, you should use DFT/TD-DFT to obtain the ground/excited/triplet state geometry and Hessians, and only use the higher-level method for the final ESD step.

Also, we recommend using APPROXADEN under the %ESD options.

%ESD	
    APPROXADEN TRUE 
END

In this case, only one single point at the geometry of the ground state needs to be done, and the adiabatic energy difference will be automatically obtained from the ES Hessian information, without the need of a second single point at the extrapolated ES geometry, which could be unstable.

5.5.8. Circularly Polarized Spectroscopies

5.5.8.1. General Aspects of the Theory

When circularly polarized (CP) light interacts with a chiral chemical structure (optically active), it differentially absorbs left and right CP lights (\(I_{LCP} \neq I_{RCP}\) ) resulting in the electronic circular dichroism (ECD). Similarly, it can differentially emit left and right CP lights leading to CP luminescence (CPL), which includes CP fluorescence (CPF) and phosphorescence (CPP) spectra.

Starting from ORCA 6, the ESD module has been expanded to include calculations of CP rates and spectra for chemical system. This enables the computation of the vibronic effect on ECD, CPF, and CPP spectra. The methodology is generally similar to the interaction of unpolarized light with matter, including absorption and photoluminescence. However, when a CP photon interacts with an optically active system, the electric field of the photon induces a linear displacement of the charge (transition electric dipole), while the magnetic field induces a circulation of the charge (transition magnetic dipole). These combined interactions cause an electron to be excited in a helical motion, involving both translation and rotation, along with their associated operators.

In a commonly use practice by defining a laboratory frame in which the z-axis defines the direction of the light trajectory, CP light interactions can be generated with the use of the complex vectors \(\mathcal{E} \pm= \frac{1}{\sqrt{2} } (\hat{x} \pm i \hat{y})\)

In this framework the FFMIO operator transforms as:

(5.31)\[ {\mathrm{T}}_{\mathrm{IF}}^\mathrm{\pm} =1/2\sum_{j=1}^{N} \left\langle\mathrm{I}\middle|\mathrm{e}^{{\mathrm{-ikr}}_\mathrm{j}} \left(\mathrm{\varepsilon\bullet}{\hat{\mathrm{p}}}_\mathrm{x}\right)\middle| \mathrm{F}\right\rangle\mathrm{\pm}\left\langle\mathrm{I} \middle|\mathrm{e}^{{\mathrm{-ikr}}_\mathrm{j}}\left(\mathrm{\varepsilon\bullet}{\hat{\mathrm{p}}}_\mathrm{y}\right)\middle|\mathrm{F}\right\rangle \]

In both ECD and CPL (CPF or CPP) spectroscopies the measured intensities are related to the difference of absorption or luminescence of the left and right polarized transition moments given by:

(5.32)\[\Delta_{IF}^{L\pm R}(k,\epsilon)={{|T}_{IF}^-|}^2\pm{{|T}_{IF}^+|}^2 \]

which leads to the following expressions for the sum and the difference of the square moduli \(|{T_{IF}^\pm|}^2\):

(5.33)\[\Delta_{IF}^{L+R}(k,\epsilon)=1/2\left\langle I\middle|\sum_{j=1}^{N}{e^{{-ikr}_j}\left(\varepsilon\bullet{\hat{p}}_x\right)}\middle| F\right\rangle\left\langle I\middle|\sum_{j=1}^{N}{e^{{-ikr}_j}\left(\varepsilon\bullet{\hat{p}}_y\right)}\middle| F\right\rangle \]

(5.34)\[\Delta_{IF}^{L-R}(k,\epsilon)=-\mathbf{Im}\left(\left\langle I\middle|\sum_{j=1}^{N}{e^{{-ikr}_j}\left(\varepsilon\bullet{\hat{p}}_x\right)}\middle| F\right\rangle\left\langle I\middle|\sum_{j=1}^{N}{e^{{-ikr}_j}\left(\varepsilon\bullet{\hat{p}}_y\right)}\middle| F\right\rangle\right) \]

Hence within the ED approximation, ECD and CPL radiative transition rates can be calculated through the orientational average of Equation (5.32), employing the Fermi’s Golden rule:

(5.35)\[ k_{ECD}\left(\omega\right)=\frac{{16\pi}^2\omega_{ECD}}{3}\ \sum_{F}\mathbf{Im}\left(\left|\left\langle\Psi_I\left|\hat{\mu}\right|\left.\Psi_F\right\rangle\right.\left\langle\Psi_F\left|\hat{m}\right|\left.\Psi_I\right\rangle\right.\right|\right)\delta\left({E_{FI}\pm\omega}_{ECD}\right) \]

(5.36)\[ k_{CPL}\left(\omega\right)=\frac{{16\omega_{CPL}}^3n^2}{3\hbar c^3}\ \sum_{F}\mathbf{Im}\left(\left|\left\langle\Psi_I\left|\hat{\mu}\right|\left.\Psi_F\right\rangle\right.\left\langle\Psi_F\left|\hat{m}\right|\left.\Psi_I\right\rangle\right.\right|\right)\delta\left({E_{FI}\pm\omega}_{CPL}\right) \]

where \(\omega_{ECD/CPL}\) are the excitation and emission CP photon energies, respectively while \(\omega_{FI}\) are the energies between the initial and final states reached in the absorption or the photoluminescent processes. Similarly \(E_{FI}\) is the transition energy and \(\delta\) refers to the line-broadening mechanism arising from the lifetimes of the relevant final states and c is the speed of light. In the above expressions \(\hat{\mu}\) defines electric dipole operator while \(\hat{m}\) is the respective magnetic dipole operator \(\hat{m}=\frac{1}{2m_ec}\sum_{i}{r_i\times\widehat{p_i}}\) and \(m_e\) is the electron mass. In the above expressions \(\mathbf{Im}\left(\left|\left\langle\Psi_I|\hat{\mu}|\left.\Psi_F\right\rangle\right.\left\langle\Psi_F|\hat{m}|\left.\Psi_I\right\rangle\right.\right|\right)\) represents the rotatory strength (\(R_{IF}\)). As discussed above the transition rates including the vibronic coupling, on the Frank-Condon (FC) and Herzenberg-Teller (HT) limits, can be efficiently proceed through the path integral approach[598] in which it is possible to calculate \(k_{ECD/CPL}^{obs}\) from the Fourier Transform (FT) of the respective correlation function \(\chi_{(t)}\) that is computed from the path integral of the multidimensional harmonic oscillator according to[610]:

(5.37)\[ k_{ECD/CPL}^{obs}(\omega)=2\alpha\mathcal{R}e\int_{0}^{\infty}\chi_{\left(t\right)}e^{\pm i\omega t}dt\]

with \(\alpha\) being a collection of constants and for CP transition one-photon rates (ECD, CPL) considering electric dipole and magnetic dipole interactions in the expression of the rotatory strengths it takes the form:[610]

(5.38)\[ \chi_{\left(t\right)}=e^{\pm i\omega t}[ \mathbf{Im}\left[\mu_em_e^\ast\right]\rho^{FC}\left(t\right) +\sum_{k}\mathbf{Im}\left[\mu_e\frac{\partial m_e^\ast}{\partial{\bar{Q}}_k}\right]\rho_k^{\frac{HT}{FC}}\left(t\right) +\sum_{k}\mathbf{Im}\left[\frac{\partial\mu_e}{\partial{\bar{Q}}_k}m_e^\ast\right]\rho_k^{\frac{HT}{FC}}\left(t\right) +\sum_{kl}\mathbf{Im}\left[\frac{\partial\mu_e}{\partial{\bar{Q}}_k}\frac{\partial m_e^\ast}{\partial{\bar{Q}}_l}\right]\rho_k^{HT}\left(t\right)] \]

where \(\mu_e\) and \(m_e\) represent the respective transition dipole \({\langle\Psi}_I|\hat{\mu}|\left.\Psi_F\right\rangle\) and magnetic dipole \(\left\langle\Psi_F|\hat{m}|\left.\Psi_I\right\rangle\right.\) moment integrals between initial and final states \(I, F\) while:

(5.39)\[ \rho^{FC}=Tr(e^{-i\hat{H}\tau}e^{-i\hat{H}\tau}) \]

(5.40)\[ \rho_k^{HT/FC}=Tr({{\bar{Q}}_ke}^{-i\hat{H}\tau}e^{-i\hat{H}\tau}) \]

(5.41)\[ \rho_{kl}^{HT}=Tr({{\bar{Q}}_ke}^{-i\hat{H}\tau}{\bar{Q}}_le^{-i\hat{H}\tau}) \]

where, these traces can be evaluated following the approach discussed in Ref[598].

Finally, it is quite commonly that the ECD and CPL spectral intensities are represented against normalized absorption and photoluminescent intensities defining, similar expressions for, the dissymmetry factors \(g_{abs}\) and \(g_{lum}\):

(5.42)\[ g_{abs/lum}\ =2\frac{I_{LCP}\ -\ I_{RCP}}{I_{LCP}\ +\ I_{RCP}}\ \ ~\ \left.\frac{4R}{D}\right|_{GS/ES\ Structure};\ \ \ -2<g_{abs/lum}<2 \]

Implying that the associated dissymmetry spectra can also be calculated, where D and R the square of the transition dipole and the rotatory strength, respectively.

5.5.8.2. Vibration effects on ECD spectra

Vertically excited (VE) computed ECD spectra are known to often be unable to describe the experiment. This is for example the case in (R) methyl oxirane. The unshifted or shifted VE ECD BP86 computed spectra do not much the experiment in terms of shape and intensity. It has been shown that these spectra need to be computed by taking into account vibronic interactions[611].

Hence following structure optimization and frequencies calculations according to the input:

!BP86 DEF2-SVP TIGHTSCF OPT FREQ
  
* xyz 0 1
C   0.02461655377138      0.08670067686058     -5.20436273663217
C   -0.23485307714882     -0.31738971302751     -3.80610272711970
O   -0.15359212444282      1.06795113221760     -4.17749263689755
H   1.05055243293426     -0.00333310016875     -5.61325012342071
H   -0.78323750369168      0.02252140387747     -5.95969728166753
H   -1.26417590138099     -0.65347889194363     -3.56065466091728
C   0.84884023150886     -0.84537627906508     -2.89604274193698
H   0.68194744925825     -0.50794125098111     -1.85197471265376
H   0.85716491819315     -1.95559179229870     -2.89420656551675
H   1.84600617099845     -0.48435690147087     -3.21751813823758
*

we can compute ESD spectrum within in VE approximation and within the ESD modules according to the following input:

!BP86 DEF2-SVP TIGHTSCF PAL4
  
%TDDFT 
NROOTS 10
END

%ESD
ESDFlag ECD
GSHESSIAN "c3h6o_opt_freq.hess "
PRINTLEVEL 2
DOHT TRUE
LINEW 500
SPECRANGE 40000, 70000
STATES 1,2,3,4,5,6,7,8,9,10
END

* xyzfile 0 1 c3h6o_opt_freq.xyz

The result is provided in Figure Fig. 5.15 where one can see that according to the expectations the computed spectrum agrees with the experiment only when FC and HT vibronic coupling schemes are taken into account

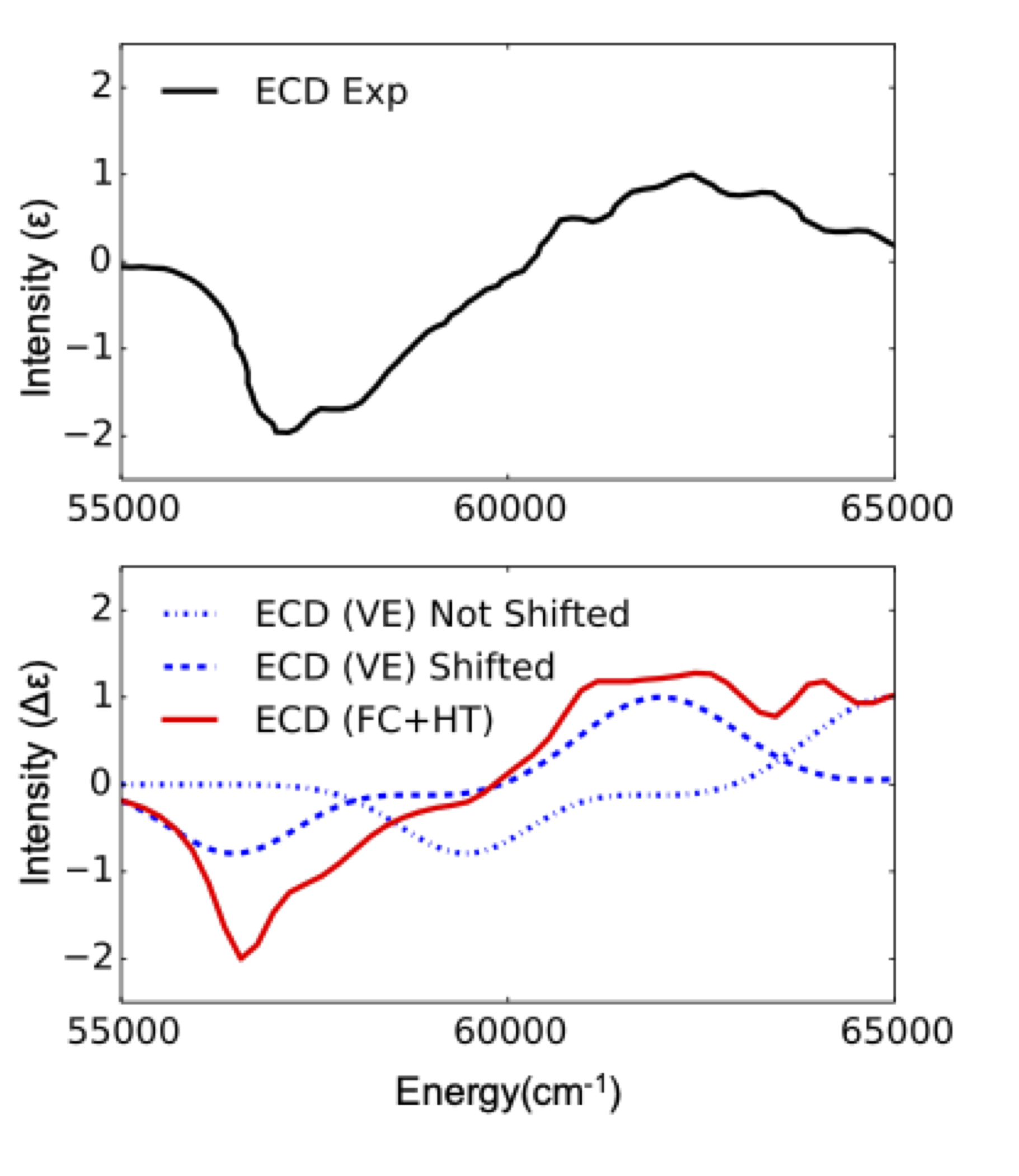
Fig. 5.15 Experimental (black) versus BP86/TDDFT (VE, blue and FC+HT red) ECD spectra for C3H6O molecule

5.5.8.3. Computation of CP-FLUOR vs CP-PHOS spectra. The case of \(C_{3}H_{6}O\).

Following the strategy described for the computation of PL (Fluorescence (PF) of Phosphorescence (PP)) spectra in the case of \(C_{3}H_{6}O\) one can also access the respective CPL and CPP spectra.

For this one needs to compute the hessian of the 1st excited singlet (ES1) and triplet states respectively (ET0) according to the following inputs

!BP86 DEF2-SVP TIGHTSCF OPT FREQ
  
%TDDFT 
NROOTS 10
IROOT 1
IMULT 1
END

* xyzfile 0 1 c3h6o_opt_freq.xyz

and

!BP86 DEF2-SVP TIGHTSCF OPT FREQ
  
%TDDFT 
NROOTS 10
IROOT 1
IMULT 3
SOCGRAD TRUE
TRIPLETS TRUE
END

* xyzfile 0 3 c3h6o_opt_freq.xyz

Then one can setup the respective PL and CPL inputs as:

PF:

!BP86 DEF2-SVP TIGHTSCF 
  
%TDDFT 
NROOTS 10
IROOT 1
IMULT 1
END

%ESD
ESDFlag FLUOR
GSHESSIAN "C3H6O_opt.hess"
PRINTLEVEL 2
DOHT TRUE 
LINEW 500
SPECRANGE 40000, 70000
END

* xyzfile 0 1 c3h6o_opt_freq.xyz

CPF:

!BP86 DEF2-SVP TIGHTSCF 
  
%TDDFT 
NROOTS 10
IROOT 1
IMULT 1
END

%ESD
ESDFlag CPF
GSHESSIAN "C3H6O_opt.hess"
PRINTLEVEL 2
DOHT TRUE 
LINEW 500
SPECRANGE 40000, 70000
END

* xyzfile 0 1 c3h6o_opt_freq.xyz

PP:

!BP86 DEF2-SVP TIGHTSCF 
  
%TDDFT 
NROOTS 10
IROOT 1
IMULT 3
DoSOC true
TRIPLETS TRUE
SOCGRAD TRUE
END

%ESD
ESDFlag PHOSP
GSHESSIAN "C3H6O_opt_freq.hess"
TSHESSIAN "C3H6O_et0.hess"
PRINTLEVEL 2
DELE 62313
DOHT TRUE
LINEW 500
TEMP  295
SPECRANGE 40000, 70000
END

* xyzfile 0 1 C3H6O_opt.xyz

CPP:

!BP86 DEF2-SVP TIGHTSCF 
  
%TDDFT 
NROOTS 10
IROOT 1
IMULT 3
DoSOC true
TRIPLETS TRUE
SOCGRAD TRUE
END

%ESD
ESDFlag CPP
GSHESSIAN "C3H6O_opt_freq.hess"
TSHESSIAN "C3H6O_et0.hess"
PRINTLEVEL 2
DELE 62313
DOHT TRUE
LINEW 500
TEMP  295
SPECRANGE 40000, 70000
END

* xyzfile 0 1 C3H6O_opt.xyz

The results are summarized in Figure Fig. 5.16

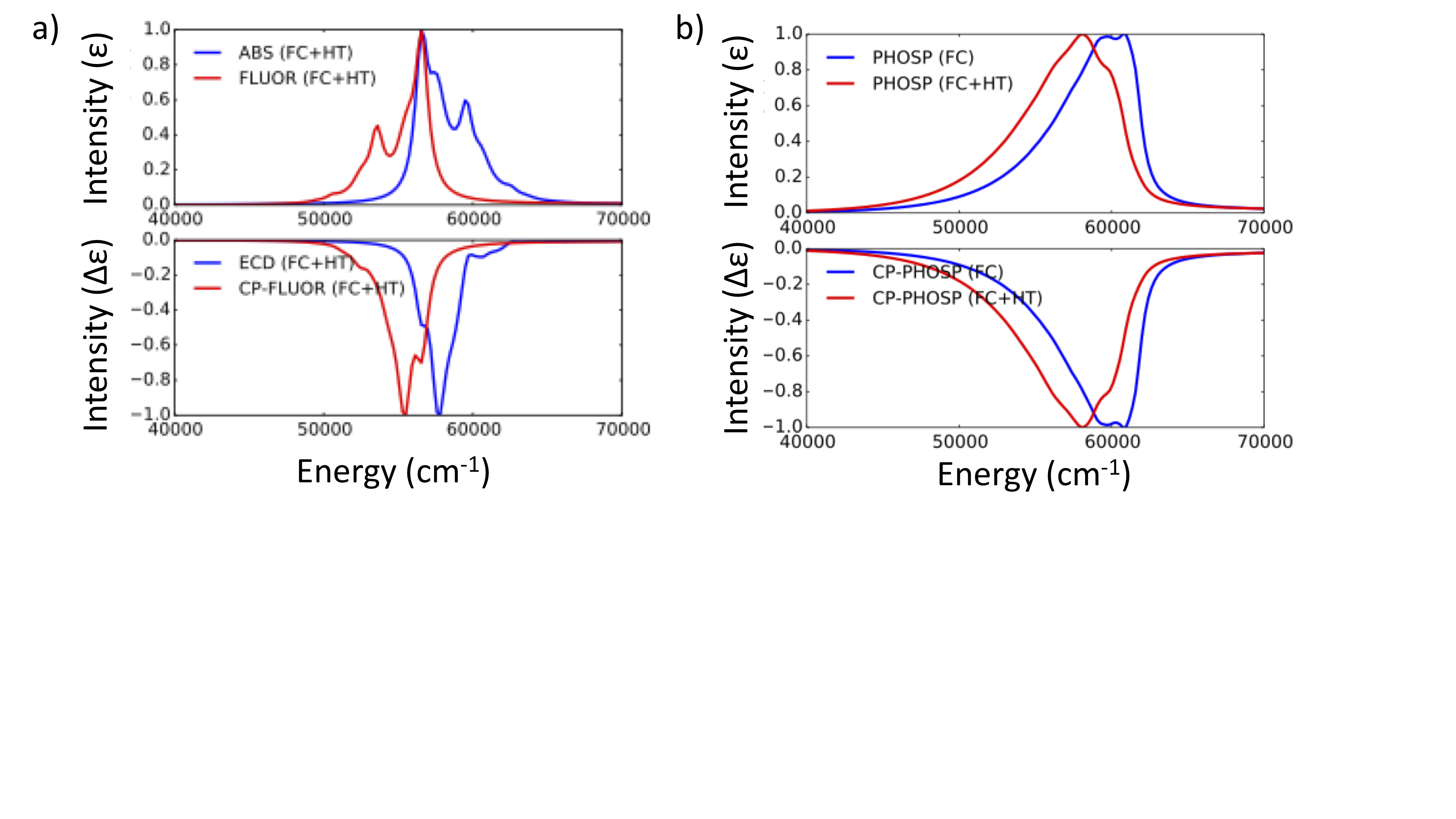
Fig. 5.16 a) Computed ABS and ECD (in blue) and Florescence and CPF (in red) under FC+HT vibronic coupling schemes b) Computed Phosphorescence and CPP under FC (in blue ) and FC+HT (in red) vibronic coupling schemes

5.5.8.4. Use of ABS, ECD PL and CPL as a routine analysis computational tools

Having at hand the possibility to compute the above spectroscopic properties quartet. Consisting of Absorption, ECD, Luminescent/Emission and CPL spectroscopies creates an arsenal of useful analysis computational tools. Let us consider a practical example from the
the N- bridged triarylamine heterohelicenoid chiral family of molecules, which are known to be very good CPL emitters in the CPL community. [612] Namely the R-, L- isomers of oxygen-bridged diphenylnaphthylamine for which both ABS ECD, PL and CPL experimental spectra are available [613]

In a first step one needs to compute to calculate the ECD and CPL spectra, this implies that one needs to optimize the ground state (GS) geometry and at least the GS hessian of both isomers, (see examples in Fluorescence Rates and Spectrum and Vibration effects on ECD spectra). Lets suppose that we have generated the GSHessian file R_OptFreq.hess file for the R-isomer Then one can employ the ESD to calculate the Absorption, ECD, Fluorescence and CPL (CPluorescecne) as follows.

For Absorption or ECD spectra a representative input is given by:

! PBE0 def2-TZVP def2/J def2-TZVP VeryTightSCF PAL8
%MaxCore 5120

%TDDFT NROOTS 5
       End

%ESD   ESDFlag     ABS or ECD
       GSHessian  "R_diphenylnaphthylamine_OptFreq.hess"
       DoHT        True
       Lines       Gauss
       InLineW     500
       STATES      1,2,3,4,5
       End

*xyz 0 1 
C           0.51103659781880     -1.54799809918165     -0.46957711710367
C          -0.67682083480241     -2.19898547218227     -0.76456508506476
C           1.59698089595014     -2.23913762447750      0.04536520831045
C           1.49004594789848     -3.60107534512753      0.24696861333386
C          -0.75027591609003     -3.56343872947031     -0.57021086417552
C           0.33765559244610     -4.27346122451739     -0.10341675327345
N           0.21984508391204     -5.66346290617628      0.07289766826829
O           2.52716581975956     -4.28847037580032      0.82258958688483
C           2.54101738078760     -5.65282427633174      0.65190453446035
C           1.43184892145219     -6.36105379222857      0.25831057061542
C           3.77147940706722     -6.27965254373750      0.89001683729049
C           3.89719111077242     -7.62085864051752      0.70851807608572
C           1.58029288205151     -7.74060974139699     -0.06585842329724
C           2.81811727341129     -8.37881977445777      0.20527726022176
O          -1.91500963727701     -4.25152600059560     -0.80702339426568
C          -2.13250715287481     -5.31470429649343      0.04909464399864
C          -1.05242665026610     -6.06056594251354      0.52598562255970
C          -3.42444532048472     -5.61905191519688      0.41037068048411
C          -3.66399173496155     -6.68754268865431      1.26210310826770
C          -1.29901325564529     -7.09753540866930      1.41085143603056
C          -2.60176522746573     -7.41491597190339      1.76502960065907
H          -4.22973438581776     -5.01558835826860      0.01489276124005
H          -4.67873778203345     -6.93777656190575      1.53843511994436
H          -0.47290745868829     -7.66765085401275      1.80929822862278
H          -2.77926863803574     -8.23774715258380      2.44386581691750
H           0.58624233693590     -0.48095844424254     -0.62562692246504
H           2.51652973024519     -1.73662559987765      0.30924801794967
H          -1.54272285055189     -1.66670869597130     -1.13102495882678
H           4.59563142014220     -5.66684912938550      1.22771972849030
H           4.83828110533620     -8.11484947410606      0.91089239524435
C           0.56233992156145     -8.49575213625774     -0.69451663429121
C           2.96252715039542     -9.75415434575818     -0.08347675768224
C           0.74593486971180     -9.81550692161063     -0.98488391710801
C           1.95147468552282    -10.46257812809982     -0.65848843248314
H          -0.36538542100730     -8.01665224889233     -0.96504181763392
H          -0.04242675451776    -10.36879326589460     -1.47770458618347
H           2.07785937833070    -11.51320955617077     -0.88255640316097
H           3.90687057621082    -10.23141194413179      0.14665882143507
*

For Fluorescence or CP Fluorescence spectra a representative input is given by:

! PBE0 def2-TZVP def2/J def2-TZVP VeryTightSCF PAL8
%MaxCore 5120

%TDDFT NROOTS 5
       End

%ESD   ESDFlag     FLUOR or CPF
       GSHessian  "R_diphenylnaphthylamine_OptFreq.hess"
       DoHT        True
       Lines       Gauss
       InLineW     500
       STATES      1,2,3,4,5
       End

*xyz 0 1 
C           0.51103659781880     -1.54799809918165     -0.46957711710367
C          -0.67682083480241     -2.19898547218227     -0.76456508506476
C           1.59698089595014     -2.23913762447750      0.04536520831045
C           1.49004594789848     -3.60107534512753      0.24696861333386
C          -0.75027591609003     -3.56343872947031     -0.57021086417552
C           0.33765559244610     -4.27346122451739     -0.10341675327345
N           0.21984508391204     -5.66346290617628      0.07289766826829
O           2.52716581975956     -4.28847037580032      0.82258958688483
C           2.54101738078760     -5.65282427633174      0.65190453446035
C           1.43184892145219     -6.36105379222857      0.25831057061542
C           3.77147940706722     -6.27965254373750      0.89001683729049
C           3.89719111077242     -7.62085864051752      0.70851807608572
C           1.58029288205151     -7.74060974139699     -0.06585842329724
C           2.81811727341129     -8.37881977445777      0.20527726022176
O          -1.91500963727701     -4.25152600059560     -0.80702339426568
C          -2.13250715287481     -5.31470429649343      0.04909464399864
C          -1.05242665026610     -6.06056594251354      0.52598562255970
C          -3.42444532048472     -5.61905191519688      0.41037068048411
C          -3.66399173496155     -6.68754268865431      1.26210310826770
C          -1.29901325564529     -7.09753540866930      1.41085143603056
C          -2.60176522746573     -7.41491597190339      1.76502960065907
H          -4.22973438581776     -5.01558835826860      0.01489276124005
H          -4.67873778203345     -6.93777656190575      1.53843511994436
H          -0.47290745868829     -7.66765085401275      1.80929822862278
H          -2.77926863803574     -8.23774715258380      2.44386581691750
H           0.58624233693590     -0.48095844424254     -0.62562692246504
H           2.51652973024519     -1.73662559987765      0.30924801794967
H          -1.54272285055189     -1.66670869597130     -1.13102495882678
H           4.59563142014220     -5.66684912938550      1.22771972849030
H           4.83828110533620     -8.11484947410606      0.91089239524435
C           0.56233992156145     -8.49575213625774     -0.69451663429121
C           2.96252715039542     -9.75415434575818     -0.08347675768224
C           0.74593486971180     -9.81550692161063     -0.98488391710801
C           1.95147468552282    -10.46257812809982     -0.65848843248314
H          -0.36538542100730     -8.01665224889233     -0.96504181763392
H          -0.04242675451776    -10.36879326589460     -1.47770458618347
H           2.07785937833070    -11.51320955617077     -0.88255640316097
H           3.90687057621082    -10.23141194413179      0.14665882143507
*

The results are summarized in Figure Fig. 5.17

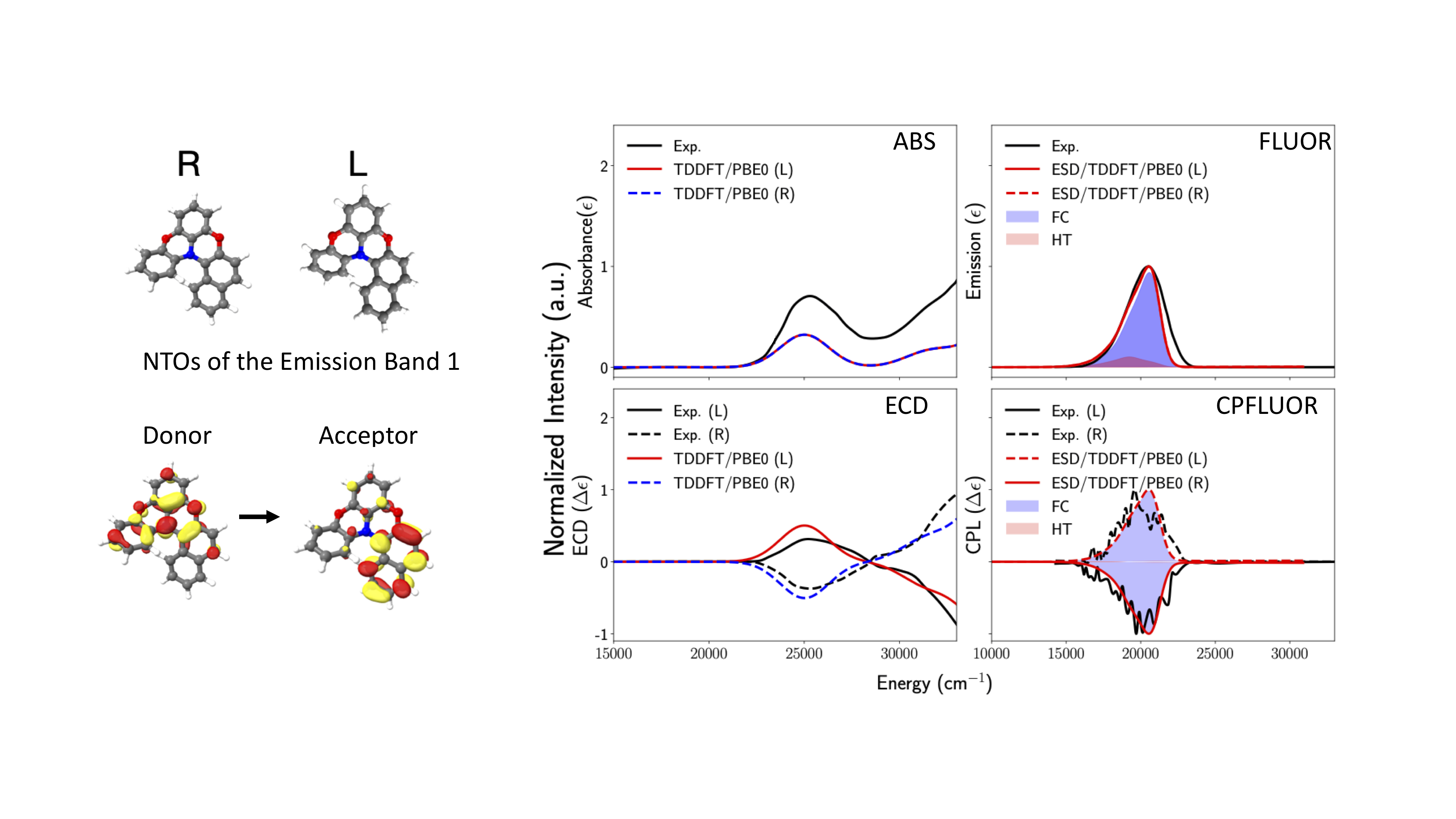
Fig. 5.17 Black Experimental vs Calculated ABS, ECD, Fluorescence and CPF spectra for R- (in blue) and L- (in red) isomers of diphenylnaphthylamine under FC+HT vibronic coupling schemes of the \(\pi\rightarrow\pi^*\) transition located at 25000 \(cm^{-1}\).

5.5.9. Magnetic Circular Dichroism

5.5.9.1. General Aspects of the Theory

The formulation presented for the calculation of the absorption spectrum may be extended to the absorption of circularly polarized light (CPL) of a system under the effect of an external magnetic field in order to compute the MCD spectrum.[614] By assuming an electric dipolar approximation under a length formulation for the light-matter interaction, the molar absorptivity contribution by the transition between an initial state i and a final state f of one fixed oriented molecule may be expressed as:

(5.43)\[ \epsilon(\omega)_{if} = \alpha \omega |\mathcal{E} \cdot \langle \Psi_i| \hat{\mu} | \Psi_f \rangle|^2 \delta(E_i - E_f \pm \hslash \omega) \]

where \(\mathcal{E}\) is the polarization vector of the incident light, and \(\alpha\) is a positive collection of constants.

By considering the case in which the light is propagating in the laboratory fixed \(\hat{z}''\) direction, the circularly polarized light is described by \(\mathcal{E} = \frac{1}{\sqrt{2} } (\hat{x}'' \pm i \hat{y}'')\) where the “\(-\)” sign corresponds to the left circularly polarized light and the “\(+\)” to the right circularly polarized light.

Similarly, as the MCD calculations presented in section Simulation of (Magnetic) Circular Dichroism and Absorption Spectra, the total absorptivity may be obtained by summing over all possible transitions and averaging the molecular orientations by using 3 rotation angles \(\theta\), \(\phi\), and \(\chi\).

(5.44)\[ \epsilon(\omega) = \alpha \omega \int_0^{2\pi}\int_0^{2\pi}\int_0^{\pi} \sum_{if} \frac{e^{- \frac{\epsilon_i}{k_B T} }}{Z} |\mathcal{E} \cdot \langle \Psi_i| \hat{\mu} | \Psi_f \rangle|^2 sin(\theta) \delta(E_i - E_f \pm \hslash \omega) d\theta d\phi d\chi \]

Considering \(\chi\) the angle which rotates the molecule in the plane perpendicular to the magnetic field perturbation (which is colinear with the incident light propagation direction), the integrals of eq. (5.44) may be computed conveniently in a seminumerical scheme by using an intermediate \(r'\) frame.

(5.45)\[ \epsilon(\omega) = \alpha \omega \sum_p w_p \sum_{if} \frac{e^{- \frac{\epsilon_i}{k_B T} }}{Z} \sum_{\beta \gamma = x',y'} \overline{\overline{\mathcal{E} }}_{\beta \gamma} \langle \Psi_i| \hat{\mu}_\beta | \Psi_f \rangle \langle \Psi_f| \hat{\mu}_\gamma | \Psi_i \rangle \delta(E_i - E_f \pm \hslash \omega) \]

where \(\theta\) and \(\phi\) values are defined by a point p in a numerical grid, \(x'\), and \(y'\) are determined by \(\theta\) and \(\phi\) values according to eq. (5.46), and \(\chi\) has been integrated analytically in the \(\overline{\overline{\mathcal{E} }}_{\beta \gamma}\) values.

(5.46)\[\begin{split} \begin{split} \hat{\mu}_{x'} &= cos(\theta) cos(\phi) \mu_{x''} + cos(\theta) sin(\phi) \mu_{y''} - sin(\theta) \mu_{z''} \\ \hat{\mu}_{y'} &= -sin(\phi) \mu_{x''} + cos(\phi) \mu_{y''} \end{split} \end{split}\]

(5.47)\[ \overline{\overline{\mathcal{E} }}_{\beta \gamma}^\pm = \int_0^{2\pi} \mathcal{E}_\beta^\pm \mathcal{E}_\gamma^{\pm*} d\chi \]

Finally, by applying the Born-Oppenheimer approximation and writing the Dirac delta function in the time domain, we get:

(5.48)\[ \epsilon(\omega) = \alpha \omega \sum_p w_p \sum_{if} \frac{e^{- \frac{\epsilon_i}{k_B T} }}{Z} \sum_{\beta \gamma = x',y'} \overline{\overline{\mathcal{E} }}_{\beta \gamma} \langle \Theta_i| \hat{\mu}_\beta^e | \Theta_f \rangle \langle \Theta_f| \hat{\mu}_\gamma^e | \Theta_i \rangle \int e^{i (E_i-E_f-\omega)t} dt \]

and by taking the difference of absorbance between left and right CPL produce we reach an expression of the MCD intensities:

(5.49)\[ \Delta \epsilon(\omega) = \epsilon^-(\omega) - \epsilon^+(\omega) = -2 \frac{\alpha}{Z} \omega \sum_{if} \sum_p w_p Im \Big[\int_{-\infty}^\infty \tilde{\chi} (t,x',y') e^{-i \hslash \omega t} dt \Big] \]

where \(\tilde{\chi}\) under a first-order approximation of the transitions moments with respect to the nuclear displacement is:

(5.50)\[ \tilde{\chi} (t,\beta,\gamma)= e^{i \Delta E t} \Big[\hat{\mu}_{0\beta}\hat{\mu}_{0\gamma}^* \rho^{FC}(t) + \sum_k \frac{\partial \hat{\mu}_{\beta} }{\partial Q_k}\hat{\mu}_{0\gamma}^* \rho^{FC/HT}(t) + \sum_k \hat{\mu}_{0\beta} \frac{\partial \hat{\mu}_{\gamma}^*}{\partial Q_k} \rho^{FC/HT}(t) + \sum_{kl} \frac{\partial\hat{\mu}_{\beta} }{\partial Q_k} \frac{\partial\hat{\mu}_{\gamma}^*}{\partial Q_l} \rho^{HT}(t) \Big] \]

Similarly, as section Simulation of (Magnetic) Circular Dichroism and Absorption Spectra, the transition moments under the effect of an external magnetic field perturbation may be estimated by using a QDPT (eq. (5.187)), and the derivatives are approximated numerically in a similar way as the ESD-Absorption case.

By applying a quasi-degenerate perturbative theory, similar to the inclusion of spin-orbit coupling effects in the phosphorescence calculations, the effect of an external magnetic field may be included in the representation of the quantum states [614]. As a result, the differential absorption of left and right circularly polarized light may be computed to obtain the vibrationally-corrected magnetic circularly dichroism spectrum. The input for the calculation is similar to the absorption case described above; nevertheless, ESD(MCD) should be used. Additionally, the intensity of the external magnetic field “B” (in Gauss) should be included, and a Lebedev grid for a semi-numerical molecular orientational average should be selected.

The method is only available with an electronic structure generated by TDDFT. The calculation supports the inclusion of Herzberg-Teller effects by setting DOHT TRUE, the ground state Hessian needs to be provided similarly to the absorption case, while the excited state Hessian can be provided or computed under a no external magnetic field approximation. An input example is:

!B3LYP DEF2-TZVP TIGHTSCF ESD(MCD) 

%TDDFT NROOTS 40
       TDA FALSE
END

%ESD    GSHESSIAN "pbq.hess"
        Hessflag AHAS
        DOHT    TRUE
        STATES 1
        B 50000.0
END

* xyzfile 0 1 pbq.xyz

Similarly, to the ESB(ABS) calculation the MCD spectrum is saved in a BASENAME.MCD file as:

Energy          TotalSpectrum           IntensityFC             IntensityHT
4817.11         -6.324671e-05           -4.528264e-06           -5.871844e-05
5026.55         -6.717718e-05           -4.809014e-06           -6.236816e-05
5235.99         -7.126386e-05           -5.100843e-06           -6.616302e-05
5445.43         -7.551756e-05           -5.404513e-06           -7.011304e-05
5654.87         -7.994996e-05           -5.720850e-06           -7.422911e-05
5864.31         -8.457379e-05           -6.050750e-06           -7.852304e-05
...

5.5.9.2. Specific Keywords and recommendations

Once selected the ESD(MCD) calculation two variables need to be defined in the %esd block:

• The intensity of the magnetic field in Gauss “B”

• The grid to make the molecular orientational average “LEBEDEVINTEGRATIONPOINTS”

The MCD signals use to be much more sensitive than the corresponding absorption intensities. As result, the MCD calculations are much more sensitive to errors in the electronic structure. So it is highly recommended to first fully understand the electronic structure problem and verify there are no important problems. In this direction we suggest the following recommendations:

• Be sure the obtained electronic states are in the correct order by assigning point group symmetry labels and comparing them with better electronic structure methods. Due to the MCD intensities emerging as a result of the interaction of states by the magnetic field perturbation, a wrong-located state in energy may affect the MCD intensities, even if it is not in the energy range you are computing. We do not recommend using the method as a black box.

• It is recommended to do first an ESD-absorption calculation on the exact same level of theory, verify the intensities and also solve any problem related to the PES representation.

• The lineshape for the best agreement of the MCD intensities compared against the experimental measurements may differ for the best value for absorption intensities.

5.5.10. Tips, Tricks and Troubleshooting

• Currently, the ESD module works optimally with TD-DFT (Sec. Excited States Calculations), but also with ROCIS (Sec. Excited States with Restricted Open-shell CIS - ROCIS), EOM/STEOM (Sec. Excited States via EOM-CCSD and Sec. Excited States via STEOM-CCSD) and CASSCF/NEVPT2 (Sec. Complete and Incomplete Active Space Self-Consistent Field (CASSCF and RAS/ORMAS) and Sec N-Electron Valence State Perturbation Theory (NEVPT2)). Of course you can use any two Hessian files and input a custom DELE and TDIP obtained from any method (see Sec. Excited State Dynamics), if your interested only in the FC part.

• If you request for the HT effect, calculating absorption or emission, you might encounter phase changes during the displacements during the numerical derivatives of the transition dipole moment. There is a phase correction for TD-DFT and CASSCF, but not for the other methods. Please be aware that phase changes might lead to errors.

• Please check the K*K value if you have trouble. When it is too large (in general larger than 7), a warning message is printed and it means that the geometries might be too displaced and the harmonic approximation might fail. You can try removing some modes using TCUTFREQ or use a different method for the ES PES.

• If using DFT, the choice of functional can make a big difference on the excited state geometry, even if it is small on the ground state. Hybrid functionals are much better choices than pure ones.

• In CASSCF/NEVPT2, the IROOT flag has a different meaning from all other modules. In this case, the ground state is the IROOT 1, the first excited state is IROOT 2 and so on. If your are using a state-averaged calculation with more than one multiplicity, you need also to set an IMULT to define the right block, IMULT 1 being the first block, IMULT 2 the second and etc.

• If using NEVPT2 the IROOT should be related to the respective CASSCF root, don’t consider the energy ordering after the perturbation.

• After choosing any of the HESSFLAG options, a BASENAME.ES.hess file is saved with the geometry and Hessian for the ES. If derivatives with respect to the GS are calculated, a BASENAME.GS.hess is also saved. Use those to avoid recalculating everything over and over. If you just want to get an ES PES, you can set WRITEHESS TRUE under

• Although in principle more complete, the AH is not NECESSARILY better, for we rely on the harmonic approximation and large displacements between geometries might lead to errors. In some cases the VG, AHAS and so one might be better options.

• If you use these .hess files with derivatives over normal modes in one coordinate system, DO NOT MIX IT with a different set of coordinates later! They will not be converted.

• Sometimes, low frequencies have displacements that are just too large, or the experimental modes are too anharmonic and you might want to remove them. It is possible to do that setting the TCUTFREQ flag (in cm\(^{-1}\)), and all frequencies below the given threshold will be removed.

• If you want to change the parameters related to the frequency calculations, you can do that under %FREQ (Sec. Vibrational Frequencies). The numerical gradient settings are under %NUMGRAD (Sec. Numerical Gradients).

• When computing rates, the use of any LINES besides DELTA is an approximation. It is recommended to compute the rate at much smaller lineshape (such as 10 cm\(^{-1}\)) to get a better value, even if the spectrum needs a larger lineshape than that.

• When in doubt, try setting a higher PRINTLEVEL. some extra printing might help with your particular problem.

5.5.11. More on the Excited State Dynamics module

ORCA has now a module designed to calculate properties related to excited states named ORCA_ESD. It can be used to predict absorption/emission spectra, transition rates, resonant Raman, and MCD spectra, based on a path integral approach to the dynamic process [598]. It has some of the functionalities of ORCA_ASA and even more, as it will be discussed. What we do here is NOT a conventional dynamics with trajectories along time points, we rather solve the equation for the transition rates or intensities depending on the different cases considered.

This formulation works because there is an analytic solution to the path integral of the Multidimensional Harmonic Oscillator and the assumption of Harmonic nuclear movement is critical. In many cases that approximation does hold and the results are in very good agreement with the experiment. The general usage of the ORCA_ESD module and some examples are already presented on Sec. Excited State Dynamics and it is recommended to read that before going into the details here. We now will discuss the specifics and keywords related to of each part of the module. A complete keyword list can be found at the end of this section.

5.5.11.1. Absorption and Emission Rates and Spectrum

5.5.11.1.1. General Aspects of the Theory

The idea behind calculating the absorption or emission rates starts with the equation from the quantization of the electromagnetic field for the transition rates between and initial and a final state:

(5.51)\[ k(\omega)_{if} = \frac{4\omega^3 n^2}{3\hbar c^3} | \langle \Psi_i | \widehat{\mu} | \Psi_f \rangle |^2 \delta(E_i - E_f \pm \hbar\omega) \]

with \(\hbar\omega\) being the energy of the photon, \(\widehat\mu\) the dipole operator and \(n\) the refractive index of the solvent, as suggested by Strickler and Berg [602].

One way to obtain \(k(\omega)\) is to compute it in the frequency domain, by calculating the Franck-Condon Factors between all initial and final states that satisfy the Dirac delta in Eq. (5.51), considering the thermally accessible initial states with the appropriate weight,

(5.52)\[ k_{}^{obs} = \int k(\omega) d\omega, \qquad k(\omega) = \sum_{if}P_i(T)k_{if}(\omega), \]

where \(P_i(T) = e^{-\frac{\epsilon_i}{k_BT} }/Z\) is the Boltzmann population of a given initial state at temperature \(T\), \(\epsilon_i\) is the total vibrational energy of state \(i\) and \(Z\) is the vibrational partition function. However, this can lead to a very large number of states to be included, particularly if there are low frequency modes. In this work we will take the a different approach and switch to the time domain, by using the Fourier Transform representation of the Dirac delta,

(5.53)\[ \delta(\omega) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} e^{i\omega t} dt, \]

so that the equation to solve, in atomic units, is:

(5.54)\[ k(\omega) = \frac{2\omega^3}{3\pi c^3Z} \sum_{if}e^{-\frac{\epsilon_i}{k_BT} } \langle\Theta_i|\vec\mu^e |\bar{\Theta}_f \rangle \langle\bar{\Theta}_f|\vec\mu^e |\Theta_i \rangle \nonumber \int e^{i(E_i-E_f - \omega)t} dt, \]

with \(\vec\mu^e\) being the “electronic transition dipole” and \(|\Theta \rangle\) the vibrational wavefunction of the initial or final state.

After some extra steps, redefinition of the time variable and insertion of a resolution of identity, it can be shown that this equation is ultimately simplified to a Discrete Fourier Transform (DFT) of a correlation function \(\chi(t)\) with a timestep \(\Delta t\), multiplied by a prefactor \(\alpha\) [598]:

(5.55)\[\begin{split}\begin{aligned} k(\omega) &= \alpha \int Tr(\vec\mu^e e^{-i\widehat{H}\tau}\vec{\mu^e} e^{-i\widehat{\overline{H} }\bar{\tau} })e^{i \Delta E t}e^{-i\omega t} dt\nonumber \\ &= \alpha \int \chi(t)e^{-i \omega t} dt\nonumber\\ &= 2\alpha \hspace{5pt} \mathfrak{Re} \int_0^{\infty} \chi(t)e^{-i\omega t} dt\nonumber\\ &\simeq 2\alpha \Delta t \hspace{5pt} \mathfrak{Re} \hspace{5pt} DFT\{\chi(t)\},\end{aligned} \end{split}\]

and this correlation function is then calculated using path integrals analytically at each time point \(t\).

If one considers that the electronic part of the transition dipole varies with nuclear displacements and we allow for it to depend on the normal coordinates (\(\mathbf{Q}\)), such as:

(5.56)\[ \vec\mu^e(\mathbf{{Q} }) = \vec\mu_0^e +\sum_{i} \left.\frac{\partial{\vec\mu^e} }{\partial{Q_i} }\right|_{\mathbf{Q}=0} Q_i + \ldots, \]

we can even include vibronic coupling or the so-called Herzberg-Teller (HT) effect. The Frank-Condon (FC) approximation keeps only the coordinate-independent term. The correlation function for the HT cases can then be derived recursively from the FC one and the calculation is done quite efficiently. It is important to say the one must choose ONE set of coordinates in order to expand the transition dipole. In our formulation, it is always that of the FINAL state and that has some implications discussed below.

Other important aspect of this theory is that, in order to solve the path integrals, one has to work in one set of coordinates, the initial (\(\mathbf{Q}\)) or the final state ones (\(\mathbf{\bar{Q} }\), with the bar indicating final coordinates). As we have a transition matrix element, one set of coordinates have to be transformed into the other and it is easy to show that they are related by

(5.57)\[ \mathbf{Q} = \mathbf{J\bar{Q} } + \mathbf{K}. \]

That was first proposed by Duschinsky in the late 1930s[601] with the Duschinsky rotation matrix \(\mathbf{J}\) and the displacement vector \(\mathbf{K}\) defined as

\[\mathbf{J} = \mathbf{L}_x^{\text{T} }\mathbf{\bar{L} }_x, \qquad \mathbf{K}=\mathbf{L}_x^{\text{T} }(\mathbf{\bar{q}_0}-\mathbf{q_0}),\]

with \(\mathbf{L}_x\) being the matrix containing the normal modes, here described in Cartesian coordinates (\(x\)), and \(\mathbf{q_0}\) begin mass weighted coordinates (\(q_i = \sqrt{m_i}x_i\)).

The program runs by first reading and obtaining the initial and final state geometries and Hessians, then computes the Duschinsky rotation matrix and displacement vector, calculates the derivatives for the transition dipoles and computes the correlation function. After that, the DFT is done and the rates are obtained and printed when necessary. As the intensities observed experimentally are proportional to the rates, the spectrum is also calculated and printed on a BASENAME.spectrum file. If PRINTLEVEL HIGH is requested under %ESD, the correlation function is also printed on a BASENAME.corrfunc file.

OBS: The units for the Emission spectra are rather arbitrary, but for Absorption they are the experimental “molar absorptivity (\(\varepsilon\))” in L mol\(^{-1}\)cm\(^{-1}\) [598]. Be aware that these are dependent on the line width of the curves.

5.5.11.1.2. Approximations to the excited state PES

As already mentioned in Sec. Excited State Dynamics, in order to predict the rates we need at least a ground state (GS) and an excited state (ES) geometry and Hessian. In ORCA, we have seven different ways to approximate this ES PES: AHAS, VH, VG, HHBS, HHAS, UFBS and UFAS. Those can can be choosen by setting the HESSFLAG under %ESD. If you actually optimize the ES geometry and input the Hessian, that will be called an Adiabatic Hessian (AH) method an no keyword must be given on the input.

OBS: In the present version, these approximations are only available for Absorption, Fluorescence and resonant Raman. They cannot be directly used for phosphorescence and ISC rate calculations. However, one can do the latter calculations by generating approximate ES Hessians from “fake” fluorescence or absorption runs, and then using the ES Hessians in AH calculations (vide infra).

The idea behind these approximations is to do a geometry update step (\(\mathbf{\Delta S = -gH^{-1} }\) for Quasi-Newton and \(\mathbf{\Delta S = -g(H+S)^{-1} }\) for Augmented Hessian) to obtain the ES structure and somehow approximate the ES Hessian. The gradient (\(\mathbf{g}\)) and Hessian (\(\mathbf{H}\)) used on the step are on column Step of Table Table 5.5 below, with a description of the final ES Hessian:

Table 5.5 Methods used to estimate the ES PES

Method	Step	ES Hessian
AHAS	ES grad + GS Hessian	calculated on the ES geometry
VH	ES grad + ES Hessian at GS geometry	calculated on the GS geometry
VG (default)	ES grad + GS Hessian	equal to GS Hessian
VGFC	ES grad + GS Hessian	equal to GS Hessian (+ APPROXADEN TRUE)
HHBS	ES grad + Hybrid ES Hessian on GS geometry	Hybrid Hessian on GS geometry
HHAS	ES grad + GS Hessian	Hybrid Hessian on ES geometry
UFBS	ES grad + Updated frequencies ES Hessian on GS geometry	Updated frequencies ES Hessian on GS geometry
UFAS	ES grad + GS Hessian	Updated frequencies ES Hessian on ES geometry

OBS: Always use the GS geometry on the input file, equal to the one in the GSHESSIAN! If you asked for OPT FREQ at the input, a .xyz file is generated with the same geometry found on the .hess. If you picked the geometry from the .hess file, remember that it is in atomic units, so you have to use BOHRS on the main input.

After the calculation of the ES PES, a file named BASENAME.ES.hess is printed and can be used in future calculations. For example, one can use it in a separate AH calculation, as if the file contains the optimized ES geometry and the exact ES Hessian (of course, in reality both are approximate). This allows one to perform e.g. phosphorescence and ISC rate calculations with approximate ES PESs even though ESD does not support these calculations directly. For example, the phosphorescence rate from a triplet state to the \(S_0\) state, with the VG approximation for the triplet PES and the ES gradient computed at the TDDFT level, can be computed as follows:

• Run an ESD fluorescence calculation using the VG approximation, but where “IROOTMULT TRIPLET” is added to the %TDDFT block. The resulting rate and spectrum are not meaningful, but the BASENAME.ES.hess file generated from this calculation is the correct VG approximation to the triplet PES.

• Run an ESD phosphorescence calculation using the AH method, with the aforementioned BASENAME.ES.hess file as the TSHESSIAN.

This way, the first ESD calculation only uses the information of the scalar triplet state in computing the VG step, while the second ESD calculation only uses the SOC-corrected states. The same ES Hessian file can therefore be used in the calculations of all three spin sublevels of the triplet state.

In addition to the BASENAME.ES.hess file, if there was any updates on the GS Hessian, like transition dipole derivatives, a BASENAME.GS.hess is also printed.

• The step can be controlled with the GEOMSTEP flag, with QN or AUGHESS options.

• Currently all ES Hessians are calculated numerically, if you want to change the parameters related to the frequency calculations, you can do that under %FREQ (Sec. Vibrational Frequencies). The numerical gradient settings are under %NUMGRAD (Sec. Numerical Gradients).

• The ES hybrid Hessian is calculated in the same way as described in Sec. Hybrid Hessian, except that the “model” Hessian is the GS one.

• The ES Hessian with updated frequencies is recalculated from the same GS normal modes, after an update on the frequencies, as \(\mathbf{H}_{up} = \mathbf{L\omega}^2_{up}\mathbf{L}^T\). With \(\mathbf{L}\) being the normal modes and \(\omega_{up}\) the updated frequencies, with negative sign being kept after the square.

• The frequencies are updated depending on a calculation of the energy after a given step. If the ES modes are equal to the GS, then a step over a coordinate \(\delta q_i\) that would result in an energy difference \(\delta E\) is given by \(\delta q_i = (-\frac{g_i}{\sqrt{\omega_i} } + \frac{\sqrt{g_i^2} }{\omega_i} + 2\delta E \omega_i)/\omega_i\). The default \(\delta E\) used is \(10^{-4}\) Eh, in general above the error of the methods. If the error in energy after the step is larger than a threshold given by the UPDATEFREQERR flag (default 0.20 or 20%), the gradients are calculated and the frequency recomputed. If not not, that mode and frequency are assumed to be the same.

• The Updated Frequencies method can greatly accelerate the calculation of the Hessian, for much fewer gradient calculation are necessary, although you do not correct the modes. Also, the derivatives over the modes are already computed simultaneously.

• The expected energy error \(\delta E\) can be changed using the UF_DELE flag.

• The default method is the VG, but the AHAS is more trustworthy for unknown systems, although a lot heavier (Sec. A better model, Adiabatic Hessian After a Step (AHAS) and [598]).

• Always check the sum of \(K_i^2\) printed on the output. If that number is too high (above 8 or so), it means that the geometries are too displaced and the theory might not work on these cases (check for different coordinate systems then, Sec. Normal modes coordinate systems).

• Also check for RMSD between the geometries after a step. If the difference is too big, there might be problems with the step.

5.5.11.1.3. Mixing methods

In principle, it is possible to use different methods to compute different parts needed for the ORCA_ESD module. You could, for instance use (TD)DFT analytical gradients for the ground/excited state geometries and Hessians and a more elaborate method such as STEOM-CCSD to get the energies and transition dipoles. If you want to do that, just input the Hessians and use the DELE flag for the energy difference between the states - at their own geometry! - and TDIP x,y,z to input the transition dipole. If there is SOC and the transition dipole is complex, use TDIP x.real, x.imag, y.real, y.imag, z.real, z.imag. The program will automatically detect each case. If you don’t input these, they will be obtained by the module during the run, so you can set the excited method you want and let the program figure out DELE and TDIP.

OBS: It is not advisable to mix different levels of theory during a geometry step though. If you obtained a GS Hessian from DFT, doing a step based on a CASSCF ES numerical gradient might not lead to reasonable results. The same would be problematic even for different DFT functionals.

5.5.11.1.4. Removal of frequencies

If, after calculating an ES Hessian you end up with negative frequencies, the calculation of the correlation function might run into trouble. The default for the module is to turn all negative frequencies positive, printing a warning if any of them was lower than -300 cm\(^{-1}\). If that is the case, you are probably on a saddle point and not even a minimum, so results should be taken with care,

You can also choose to completely remove the negative frequencies (and the corresponding from the GS), by setting IFREQFLAG REMOVE or leave them as negative with IFREQFLAG LEAVE under %ESD.

Sometimes, low frequencies have displacements that are just too large (check on the \(\mathbf{K}\) vector), or the experimental low frequency modes are too anharmonic and you might want to remove them. It is also possible to do that setting the TCUTFREQ flag (in cm\(^{-1}\)), and all frequencies below the given threshold will be removed.

5.5.11.2. Normal modes coordinate systems

When working with systems with weak bonds, such as hydrogen bonds and \(\pi\) stacking, or with biphenyls and similar planar molecules it is common that there will be low frequency-high amplitude modes related to the angular bending. It has been shown that, in some cases, the normal modes transformed from Cartesian coordinates might be not sufficient to describe systems with these large amplitude motion [615]. In those, the definition of normal modes in terms of some curvilinear set of coordinates such as the internal ones are more suitable.

The first order transformation from Cartesian (\(\mathbf{x}\)) to internal (\(\mathbf{s}\)) coordinates is given by Wilson’s \(\mathbf{B}\) matrix[616] as

(5.58)\[ \mathbf{s} = \mathbf{B(x-x_0) }, \]

and here we use Baker’s[617] delocalized internal coordinates as default. First, a redudant set is build and an singular value decomposition of the \(\mathbf{G} = \mathbf{BB}^T\) matrix is performed to obtain the non-redundant set. The latter can be generated by \(\mathbf{B' = U}^T\mathbf{B}\), where \(\mathbf{U}\) are the eigenvectors correponding to non-zero eigenvalues of \(\mathbf{G}\). Then an orthogonal set is contructed from \(\mathbf{B'' = G'}^{-1/2}\mathbf{U}^T\mathbf{B}\). As the eigenvectors are not conitnuous functions of the coordinates, in order to avoid using an arbitrary selection, we will follow the work of Reimers[618] and set \(\mathbf{G}^{-1/2}\mathbf{U}^T = \mathbf{\bar{G} }^{-1/2}\mathbf{\bar{U} }^T\), or use the same transformation for the initial an final coordinates. Please note that this may lead to numbers larger than 1 on the Duschinsky rotation matrix, for it is an approximation and the calculated rates may vary a little. The normal modes in internal coordinates (\(\mathbf{L}_s\)) are then obtained from those in Cartesian ones (\(\mathbf{L}_x\)) as

(5.59)\[ \mathbf{L}_s = \mathbf{B''M}^{1/2}\mathbf{L}_x, \]

and the Duschinsky relation ((5.57)) still holds[615], with the displacement vector being simply

(5.60)\[ \mathbf{K}_s = \mathbf{L}_s^T(\mathbf{\bar{s} } - \mathbf{s}). \]

The options available for coordinate systems can be set under COORDSYS, and can be CARTESIAN, INTERNAL (for Baker delocalized - default), WINT (for weighted internals following Swart and Bickelhaupt [619]), FCWL (force constant weighted following Lindh [620]) and FCWS (same as before, but using Swart’s model Hessian).

OBS: Calculating in internal coordinates is usually better but not necessarily. If something goes wrong, you may also want to try the Cartesian option.

5.5.11.2.1. Geometry rotation and Duschinsky matrices

The electronic transition should not to take place simultaneously with translations and rotations[621] of the molecular structure. Before further calculations take place, the initial and final state structures are superimposed to satisfy Eckart’s conditions by obtaining a rotation matrix \(\mathbb{B}\) that ensures \(\sum m_i(\mathbb{B}\mathbf{R_i} \times \mathbf{\bar{R}_i})=0\) [622], with \(\mathbf{R}\) being Cartesian coordinates. As the initial geometry is rotated, so must be the corresponding normal modes \(\mathbf{L}_x\) also. This can be turned of by setting the flag USEB FALSE.

By the default the Duschinsky rotation matrix is set to Identity, to take advantage of our much faster algorithm. To turn that on, just set USEJ TRUE. You can check the “diagonality” of this matrix by looking at the Diagonality Index (DI), here defined as \(\sqrt{\sum_i \mathbf{J}_{ii}^2 / \sum_{ij}\mathbf{J}_{ij}^2}\). A DI=1 would be a perfectly diagonal matrix. The amount of mixing between modes is rpresented by the Mixing Index, with is here is given by \(\langle |J_{max}| \rangle\), or the average value of the maximum \(J_i\) of each line. If DI=1, it means each normal coordinate from the initial state is equal to a mode of the final state. When USEJ=TRUE, the largest components of the \(\mathbf{J}\) matrix are printed along with the \(\mathbf{K}\) vector, so you can have a better idea of how the mixing is occuring.

5.5.11.2.2. Derivatives of the transition dipole

The derivatives of the transition dipoles with respect to the normal coordinates of the final state can be obtained directly from the derivatives with respect to the Cartesian coordinates as

(5.61)\[ \mathbf{U}(\mathbf{\bar{Q} }) = \mathbf{\bar{L} }_x^T \mathbf{M}^{-1/2} \mathbf{U(\bar{R} }), \]

\(\mathbf{U}\) being the matrix of the x,y and z components of the derivative, \(\mathbf{M}\) a \(3N\times 3N\) matrix with the atomic masses along the diagonal. Also, in case one already has the derivatives with respect to the initial state , those can be transformed into the derivatives with respect to the final state by using the Duschinsky relation, assuming that \(\vec\mu^e_0(\mathbf{\bar{Q} }) + \sum_i \frac{\partial \vec\mu^e}{\partial \bar{Q}_i}\bar{Q}_i = \vec\mu^e_0(\mathbf{Q}) + \sum_i \frac{\partial \vec\mu^e}{\partial Q_i}Q_i\), so that

(5.62)\[ \frac{\partial \vec\mu^e}{ \partial \bar{Q}_k} = \sum_j \mathbf J_{jk}\frac{\partial \vec\mu^e}{\partial Q_j}. \]

By default, this transformation is NOT done, since Eq. (5.62) is an approximation. If you want to turn it on, set CONVDER TRUE under %ESD.

OBS: Remember that, if you already have the Cartesian derivatives over the final state, like if you use AHAS for an absorption spectrum, the conversion should be exact (although there might be numerical issues, always use a larger GRAD for frequencies!).

Alternatively, these can be calculated numerically from displacements over each normal mode. In this case, it is convenient to use the dimensionless normal coordinates \(q_i = \omega_i^{1/2}Q_i\) which represent proportional displacements on the PES [623]. We use \(\Delta q = 0.01\) by default, but this can be changed setting the DER_DELQ flag.

• Again, DO NOT MIX different coordinates systems. If the derivatives were calculated over one coordinate set and you decide to change it, it has to be recalculated. You can manually delete them from the BASENAME.ES.hess file.

• For hybrid functionals, you can choose to use DFT for the gradient, energy and transition dipole, and the fast simplified TDA (Sec. Simplified TDA and TD-DFT) only for the derivatives by seting STDA TRUE under %ESD.

• A simple trick can be used to accelerate the computation of derivatives. If the first displacement gives a transition dipole that is too close to the reference, then the derivative can be assumed to be small and just the plus displacement may be taken to compute the derivative (with an usually small error). If it is large enough, then the minus displacement is also done and central differences is used. This is the default method and can be turned off by setting FASTDER to FALSE.

• The central differences option can be altogether turned off by setting CENTRALDIFF FALSE under %ESD.

• If you are having problems, set a larger PRINTLEVEL to check the individual calculation of the derivatives, you might be having some kind of root flipping during the displacement, or some other issue.

5.5.11.2.3. The Fourier Transform step

After the calculation of the correlation function, it is necessary to do a Fourier Transform (FT) step. To do that numerically, it is needed to correctly choose the grid in wich the time points will be computed, for that affects how the results will be obtained in the frequency domain. We have developed a method to generate an optimal set of parameters, depending on the final spectral resolution desired [598] and it will be used by default. Even so, you can choose your own grid by setting the NPOINTS and MAXTIME (in atomic units!) flags under %ESD. There are a few comments related to that:

• Because we solve the FT using a very efficient Cooley-Tukey algorithm, the NPOINTS should be always multiple of two. You can put any number on the input, but the next larger multiple of two will be calculated and set.

• The MAXTIME should be enough so that the correlation function goes to zero. If anything goes wrong, please check the BASENAME.corrfunc file for that.

• The finer the spectral resolution chosen with SPECRES, the largest MAXTIME must be.

• If you have a larger MAXTIME, you also must increase NPOINTS, otherwise the grid will be too sparse and many oscillations will be skipped.

5.5.11.2.4. Spectrum options

The final spectrum is saved in a BASENAME.spectrum file, with the total spectrum, the FC and HT parts discriminated, as explained in Sec. Excited State Dynamics. He are some detailed about it:

• The range for which the spectrum is saved is given by default, but it can be set using SPECRANGE flag under %ESD, as SPECRANGE 10000,70000.

• All of the INPUT units should always be in CM-1, but you can choose the OUTPUT units by setting the UNIT flag to CM-1, NM or EV.

• In order to better converge the correlation function and approximate experimental spectra, a lineshape function can be used instead of the delta. The default is to use a LOREZENTIAN lineshape, but LINES can be set to DELTA, LORENTZ, GAUSS or VOIGT.

• The DELTA lineshape might lead to a correlation function that oscillates forever, so please take care with that option.

• The default line widths are LINEW 50 and INLINEW 250.

• If you use a VOIGT lineshape, the Gaussian width can be controlled separately using the INLINEW flag. By default, it will be proportial to the Lorezntian to reach the same FWHM.

• The LINEW and INLINEW are NOT the full width half maximum (\(FWHM\)) of these curves. However they are related to them by: \(FWHM_{lorentz} = 2\times LINEW\) and \(FWHM_{gauss} = 2.355 \times INLINEW\). For the VOIGT curve, it is a little more complicated but in terms of the other FWHMs, it can be aproximated as \(FWHM_{voigt} = 0.5346\times FHWM_{lorentz} + \sqrt{(0.2166\times FWHM_{lorentz}^2 + FWHM_{gauss}^2) }\).

• The resolution of the spectrum can be modified with the SPECRES flag. By default it is a fraction of the LINEW. Please be aware that higher resolution (smaller SPECRES), mean a larger grid for the correlation function and more time points to calculate on.

5.5.11.2.5. General

• The temperature is accounted for exactly on Absorption and Emission [598] and can be set using the TEMP flag.

• PRINTLEVEL can be set to HIGH in order to print more details, including Huang-Rhys factors which are useful for rationalizing the contribution of different vibrational modes to the rate/spectrum.

• The frequencies read from the Hessian files can be scaled by any number by setting the SCALING flag under %ESD. The default is 1.0.

• If necessary, the transition dipole can also be scaled by setting the TDIPSCALING flag.

• If you just want to compute an ES PES and stop, set WRITEHESS to TRUE and the correlation function will be skipped.

• In order to make use of the fastest algorithm, set SAMEFREQ to TRUE and the DO method will be used, assuming equal Hessians between initial and final states and maximizing the efficiency when calculating the correlation function.

• If you want to calculate phosphorescence rates, you MUST input the adiabatic energy difference DELE manually (the energy difference between each state at its own geometry). And, of course, don’t forget to set the SOC module to true.

5.5.11.3. Intersystem crossing rates

5.5.11.3.1. General Aspects of the Theory

Intersystem crossing (ISC) rates between a given initial state \(i\) and a final state \(f\) can be calculated from Fermi’s Golden rule:

(5.63)\[ k(\omega)_{if} = \frac{2 \pi}{\hbar} | \langle \Psi_f | \widehat{H}_{SO} | \Psi_i \rangle |^2 \delta(E_i - E_f), \]

which is quite similar to the Eq. (5.51) for Fluorescence, except for the frequency term. The same trick used there can be applied here to swtich to the time domain. Then, we are left with a simple time integration, which is not anymore difficult to solve than the equations above.

One can use all of the infrastructure already presented to compute these ISC rates, including Duschisnky rotation, vibronic coupling effects, use of different coordinate systems and so on. Right now, its use is optimized for CIS/TDDFT, as explained in Section Intersystem Crossing Rates (unpublished), but it can be applied in general by combining simpler methods to obtain the geometries and Hessians with more advanced methods to compute the SOC matrix elements, when needed.

5.5.11.3.2. Tips and Tricks

• The DELE must be given when using ESD(ISC), it is not automatically computed.That is the energy of the initial state minus the energy of the final state, each at its own geometry.

• A SOC matrix element calculated from any method can be given on the input using the SOCME Re, Im flag, where these are the real and imaginary parts of that number.

• The SOCMEs from TD-DFT are not bad, maybe except for those between the ground singlet and the triplets. In that case, a multireference calculation might be the preferred option.

• If the final state is higher in energy than then initial state, the DELE is a negative number. In that case, there is barrier to go up when doing the ISC and the rates becomes more sensitive to the temperature.

• In contrast to Fluorescence, the ISC rates depend strongly on the inclusion of Duschisnky rotations, please take care when using USEJ FALSE.

• The default LINES is GAUSS, and the default INLINEW of 250 \(cm^{-1}\) might be too large. One should always investigate it by varying the width a bit. Other LINES can increase the error, please take care when changing it.

5.5.11.4. Resonant Raman Spectrum

5.5.11.4.1. General Aspects of the Theory

Raman intensities can be obtained in many different ways, depending on the experimental set up. As discussed extensively by D. A. Long [607, 608], the part of it that is “set up independent” is the Scattering Factor (or Raman activity), given by:

(5.64)\[ S = 45a^2 + 7\gamma \hspace{10 pt} \left( \frac{C^2 m^2}{amu V^2} \right), \]

where the \(a\) is related to the isotropic part of the “transition polarizability” between an initial state and a final state with a different vibrational quantum number \(\langle \Psi_f| \hat{\alpha} | \Psi_i \rangle = \alpha_{if}\):

\[a = \frac{1}{3}|(\alpha_{xx}+\alpha_{yy}+\alpha_{zz})|\]

and \(\gamma\) is also related to its off-diagonal elements:

\[\gamma = \frac{1}{2} [|(\alpha_{xx}-\alpha_{yy})|^2 + |(\alpha_{yy}-\alpha_{zz})|^2 + |(\alpha_{zz}-\alpha_{xx})|^2 +6(|\alpha_{xy}|^2 + |\alpha_{yz}|^2 + |\alpha_{xz}|^2)].\]

This transition polarizability itself can be computed using Kramers, Heisenberg and Dirac (KHD) formalism and it can be shown that each of its Cartesian components can be calculated as a sum-over-states:

(5.65)\[ \alpha_{\rho\sigma}^{if} = \frac{1}{\hbar} \sum_{n \neq i,f} \left( \frac{\langle \Psi_f | \mu_\rho | \Psi_n \rangle \langle \Psi_n | \mu_\sigma | \Psi_i \rangle }{\Delta E_{ni} - \omega_{laser} + i\gamma_{lt} } + \frac{\langle \Psi_f | \mu_\rho | \Psi_n \rangle \langle \Psi_n | \mu_\sigma | \Psi_i \rangle }{\Delta E_{ni} + \omega_{laser} + i\gamma_{lt} } \right) \]

In (5.65), the sum is over any number of electronic excited states \(n\), \(\Delta E_{in}\) is the energy difference between the initial state and the excited, \(\omega_{laser}\) is the laser energy and \(\gamma_{lt}\) is the lifetime broadening to avoid a zero on the denominator. If we work with a laser for which the frequency is close to the excited state energy difference, the first term is much larger than the second and can approximate alpha by

(5.66)\[ \alpha_{\rho\sigma}^{if} \simeq \frac{1}{\hbar} \sum_{n \neq i,f} \left( \frac{\langle \Psi_f | \mu_\rho | \Psi_n \rangle \langle \Psi_n | \mu_\sigma | \Psi_i \rangle }{\Delta E_{ni} - \omega_{laser} + i\gamma_{lt} } \right). \]

This equation can be solved using a path integral approach by switching to the integral form of \(1/x\):

(5.67)\[ \frac{1}{x} = \frac{i}{\hbar} \int_0^{\infty}e^{-ixt/\hbar}dt \]

So that the components of \(\alpha_{if}\) can be given by:

(5.68)\[ \alpha_{\rho\sigma}^{if} \simeq \sum_{n \neq i,f} \frac{i}{\hbar^2}\int_{0}^{\infty}\langle \Psi_f | \mu_\rho | \Psi_n \rangle \langle \Psi_n | \mu_\sigma | \Psi_i \rangle e^{-it(\Delta E_{in} - \omega_{laser} - i\gamma_{lt}) }dt \]

From here on, it is possible to show that the \(\alpha_{\rho\sigma}^{if}\) can be calculated as an integral of a correlation function [607], which is similar to the one previously discussed. In order to calculate that, a path integral scheme is also used and a geometry and Hessian for the ES are needed. The ORCA_ESD module predicts the ES PES (if not inputed), computes the \(\alpha_{if}\) and then prints the Scattering factor on a spectrum named BASENAME.spectrum.LASERE.

OBS.: The actual Raman Intensity collected with any polarization at 90 degrees, the I(\(\pi/2; \parallel^{s}+\perp^{s},\perp^{i}\) [608]), can be obtained by setting RRINTENS to TRUE under %ESD.

OBS2.: In the current implementation, if a multistate calculation is requested, Eq. (5.66) is solved for each state and all spectra are summed up afterwards.

5.5.11.4.2. Specific Keywords and Details

In order to solve Eq. (5.68), the same information as for Absorption/Emission is needed and to compute the ES PES all of the above approximations are also valid. The main difference here is that a laser energy, given by the LASERE flag, should be given. If it is not given, the default is to set it to the 0-0 energy difference between the ground and the excited state. As mentioned before, more information can be found on Sec. Resonant Raman Spectrum.

• You can choose more than one laser energy by setting LASERE 1,2,3,4 and etc. If so, each spectrum will be saved on a different BASENAME.spectrum.LASERE file.

• You can also choose more than one excited state to be accounted for with the flag STATES 1,2,3, etc. and the final spectrum will be the sum of all of Scattering Factors given by the \(\alpha_{if}\)s. You can NOT choose several states and laser energies currently.

• The automatic selection for the integral grid is also done based on the same ideas as mentioned before.

• The default lineshape for resonant Raman is VOIGT.

• The lineshape of the RR spectra will be taken from the RRSLINEW flag. In this case, LINEW and INLINEW are used only in the calculation of the correlation function.

• Currently the only temperature for which this model works is at 0K.

• In terms of which vibrationally excited states to be considered, currently it goes up to Raman Order 2, which means fundamentals, first overtones and combination bands (up to a total quantum number of 2). You can reduced that using RORDER flag.

• It is also possible to include HT effect here for weak transitions, but be aware the calculation is much more costly. Due to technical reasons, the data is saved only on memory so, if you plan to go being 300 modes and do HT, there should be A LOT of memory available, about \(8 \times NMODES^4\). Also, you should expect a VERY long time for the computation of the correlation function. We are currently working on ways to accelerate this particular case.

• As it is explained on the reference paper [607], the calculations using both Duschinsky rotation and HT effect can be greatly accelerated setting cutoffs for the derivatives and J matrix elements. The RRTCUTDER is a ratio with respect to the transition dipole moment below which the derivatives will be ignored and RRTCUTJ is a cutoff for J matrix elements. As the paper suggests, RRTCUTDER = 0.001 and RRTCUTJ = 0.01 are in general good numbers. We do recommend using these, but please be aware of the specific needs of your system.

5.5.12. Complete Keyword List for the ESD Module

%ESD                             #The booleans are the defaults
  ESDFLAG    ABS   (default)     #Which calculation to make?
             ECD
             FLUOR (default)
             CPF/CPFLUOR
             PHOSP
             CPP/CPPHOSP
             MCD                 #Only available with TDDFT
             RR 
             ISC
             IC

  GSHESSIAN  "BASENAME.hess"     #The ground state Hessian
  ESHESSIAN  "BASENAME_S1.hess"  #The excited state Hessian
  TSHESSIAN  "BASENAME_T.hess"   #The triplet state Hessian

  HESSFLAG   AHAS                #How to obtained the ES PES?
             VH
             VG (default)
             VGFC                # VG + APPROXADEN TRUE
             HHBS
             HHAS
             UFBS
             UFAS

  STATES     1,2,3,4             #IROOTS to compute

  MODELIST   4,5,6               # only include the 4th, 5th and 6th vibrational modes
                                 # in the ESD calculation
  SINGLEMODE 1,5,10              # run three ESD calculations, each considering only
                                 # one of the 1st, 5th and 10th vibrational modes

  DOHT       FALSE               #Do HT effect?
  FASTDER    TRUE                #Use the fast derivatives algorithm?
  DELQ       0.01 (default)      #Dimensionless displacemente for derivatives
  STDA       FALSE               #Use sTDA during derivatives?

  APPROXADEN FALSE               #Compute the DELE by extrapolating info from
                                 #the Hessians, avoiding second single-point 
                                 #at the ES geometry                

  USEJ       FALSE               #Consider Duschinsky rotations?
  USEB       TRUE                #Rotate the initial state?
  SAMEFREQ   TRUE                #Use DO method and J=1.

  DELE       12000               #Custom energy difference
  TDIP       x,y,z               #Custom transition electric dipole
             x.re,x.im,y.re,y.im,z.re,z.im
  TMDIP      x,y,z               #Custom transition magnetic dipole
             x.re,x.im,y.re,y.im,z.re,z.im
  SOCME      x.re,x.im           #Custom spin-orbit coupling matrix elements, in a.u.
  LASERE     34000               #The laser energy for RR

  B          3000.0              #Magnetic field in Gauss for MCD
  LEBEDEVINTEGRATIONPOINTS 14    #Lebedev Grid for MCD molecular
                                 #orientational average

  GEOMSTEP   AUGHESS (default)   #Geometry step?
             QN
  STEPSCALING  1.0               #A number for scaling the steps
  STEPCONSTR   0,2,5             #A list of atoms that will not be moved
  COORDSYS   CART                #Coordinate system for the normal modes?
             INT (default)
             WINT
             FCWL
             FCWS

  TCUTFREQ   100                 #Cutoff for frequencies
  IFREQFLAG  POSITIVE (default)  #What to do with negative frequencies?
             LEAVE
             REMOVE

  UF_DELE    1E-4                #Energy difference for updated freq.
  UFFREQERR  0.2                 #Tolerated percentual error

  TEMP       298.15 (default)    #Temperature to consider
  UNIT       WN                  #wavenumbers  (Output units - input still in cm-1!)
             NM                  #nanometers
             EV                  #electron volts
  CENTRALDIFF  TRUE              #Central differences?
  CONVDER    FALSE               #Convert derivatives between state
  SCALING    1.0 (default)       #Scaling for frequencies
  TDIPSCALING  1.0 (default)     #Scaling for the transition dipole

  LINES      DELTA               #The lineshape function
             LORENTZ (default)
             GAUSS
             VOIGT (default for RR)
  LINEW      50 (default)
  INLINEW    250 (default)
  RRSLINEW   10 (default)
  
  RORDER     2 (default)         #The Raman Order for RR
  RRINTENS   false               #Calculate the intensities instead
  RRTCUTDER  0 (default)         #A cutoff for derivatives
  RRTCUTJ    0 (default)         #A cutoff for J matrix elements

  WRITEHESS  FALSE               #Make ES PES and leave

  MAXTIME    12000               #Max time (atomic units!) for the FT
  NPOINTS    131072              #Total number of points

  SPECRANGE  10000,50000         #Spectral range
  SPECRES    1.0                 #Spectral resolution
    
  PRINTVIB   FALSE               #Save a .xyz file per each vibational mode.
                                 #(Requires DOHT true)
  PRINTLEVEL 0                   #If set to 1 (or 2, 3, ...), prints additional
                                 #details of the calculation
END