Relativistic corrections#

When calculating properties or geometries of systems that contain heavy elements (fourth row and beyond), relativistic effects can have a big impact and should not be ignored. There are even studies that show that for some third row elements, relativistic effects can become significant.

Currently, there are four methods that can be used in ORCA to include that

Effective core potentials (ECPs)
Zeroth-Order Regular Approximation (ZORA, [Baerends1996])
Douglas-Kroll-Hess (DKH, [Kroll1974] [Hess1985]) Hamiltonians of first and second order
spin-free variant of exact two component treatment (X2C, [Weigend2013])

They are somewhat different and have specific strengths - so one should consider the results carefully - but maybe the most widely used is ZORA and its variants.

Effective Core Potentials (ECPs)#

Pseudopotentials or effective core potentials are a very convenient and efficient way to treat relativistic effects. They replace the core electrons with an effective potential that may cover relativistic effects by parameterization. Another benefit of ECPs is the reduced number of electrons that have to be treated explicitly, thus reducing the computation time. One of the most prominent and robust ECP families are the def2-ECPs by Dolg and co-workers.[Dolg2000] These are usually used in combination with the matching def2 basis sets by Ahlrichs.[Ahlrichs2005] Within ORCA these are automatically used if the respective basis set is requested. For example, if the def2-TZVP basis is used for a Hg atom the output will indicate the use of the respective ECP.

!wB97X-V def2-TZVP

*XYZ 0 1 
Hg 0 0 0
*

-------------------------
ECP PARAMETER INFORMATION
-------------------------

 Group 1, Type Hg ECP Def2-ECP (replacing 60 core electrons, lmax=3)

ECPs can further be assigned individually in the %basis block

%basis
  ECP       "def2-ECP"     # All heavy elements for which the ECP is defined
  NewECP Pt "def2-SD" end  # Different ECP for Pt
end

Here, we defined the def2-ECP to all heavy elements and replaced it by the def2-SD ECP only for platinum.

Note

Many different ECP options are available within ORCA. However, the usage of ECPs is still an approximation that has to be made with care. A recent study by Head-Gordon [Head-Gordon2023] and co-workers discusses various ECP families and their strengths and weaknesses.

Warning

ECPs should never be used when core properties like NMR chemical shielding tensors are calculated!

Scalar Relativistic Hamiltonians (ZORA/DKH/X2C)#

An explicit relativistic treatment of the core electrons with scalar-relativistic Hamiltonians like ZORA, DKH, or X2C is also possible. These can easily be envoked by the simple input keywords ZORA, DKH, or X2C:

!PBE0 D4 ZORA ZORA-DEF2-TZVP

!PBE0 D4 DKH DKH-DEF2-TZVP

!PBE0 D4 X2C X2C-TZVPALL

Note that here we are using specific basis for each method, named ZORA- or DKH-DEF2-TZVP, and X2C-TZVPALL. This is necessary because these basis have been specifically designed for these all-electrons calculations, and the relativistic correction should NOT be used together with the regular basis or pseudopotentials. For a detailed description of options, please check the ORCA manual.

RI and ZORA/DKH/X2C#

If you want to use any of the RI methods to accelerate the SCF, another set of special /J basis has to be used:

!PBE0 D4 ZORA ZORA-DEF2-TZVP RIJDX SARC/J

!PBE0 D4 DKH DKH-DEF2-TZVP RIJDX SARC/J

!PBE0 D4 X2C X2C-TZVPALL RIJDX X2C/J

For instance, the SARC/J auxiliary basis can be used for all the ZORA or DKH-DEF2 basis. If no specific basis is available, then one can always use AUTOAUX to automatically generate one.

Important

The SARC/J basis were optimized for RI on the SCF part, not the MP2 or higher-level correlated methods! For correlation specific /C basis consult the ORCA manual and in case of abscence use !AUTOAUX.

Example 1: the Hg dimer#

Let's test the impact of these effects on the Hg dimer, that has an experimental bond length of \(3.69 Å\) [Sattler2017].

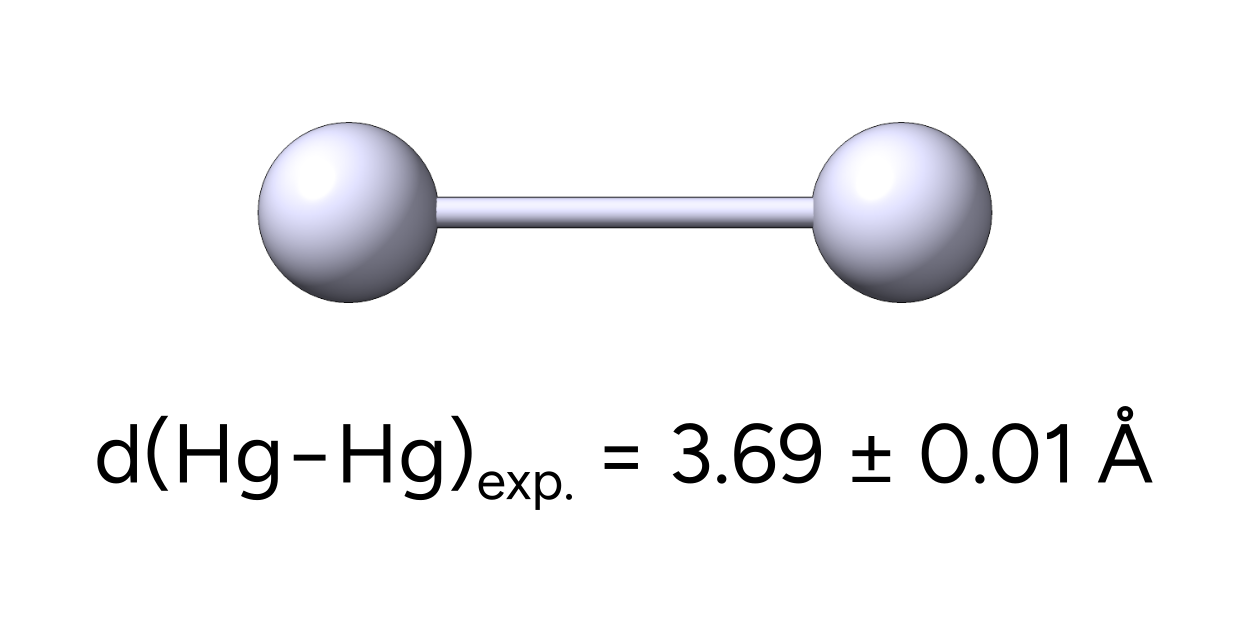
The geometry can be optimized at a regular DFT level using the DEF2-TZVP basis, that makes use of pseudopotentials or using the all-electron Hamiltonians with matching basis sets:

!PBE0 D4 DEF2-TZVP OPT

*XYZ 0 1
Hg 0 0 0
Hg 0 0 3
*

!PBE0 D4 ZORA SARC-ZORA-TZVP SARC/J OPT

!PBE0 D4 DKH2 SARC-DKH-TZVP SARC/J OPT

!PBE0 D4 X2C x2c-TZVPall X2C/J OPT

Note

The auxiliary basis for the RIJ approximation used during the relativistic case here was chosen as the appropriate SARC/J.

We can now compare the obtained Hg-Hg bond lengths to the experimental value of 3.69 Å.

Relativistic treatment	d(Hg-Hg) / Å
ECP	3.64
ZORA	3.58
DKH2	3.55
X2C	3.49
Exp.	3.69

In this case, the geometry optimized with the ECP basis set is closest to the experimental value. In general, all relativistic treatments drastically improve the agreement compared to a non-relativistic all-electron calculation. This also shows, that ECPs are in many cases sufficient to optimize geometries.

Warning

Geometry optimizations using relativistic corrections turn on by default a one-center approximation by default, that changes the energy values. Do not compare single point energies from those you obtain from an !OPT run, these numbers are be incompatible.

Example 2: ¹¹⁹Sn NMR#

In this example, we calculate the ¹¹⁹Sn NMR chemical shift with different relativistic treatments. To do so, we calculate the magnetic shielding tensors of the reference molecule SnMe₄ and the investigated teravalent tin compound with the B97M-V functional.

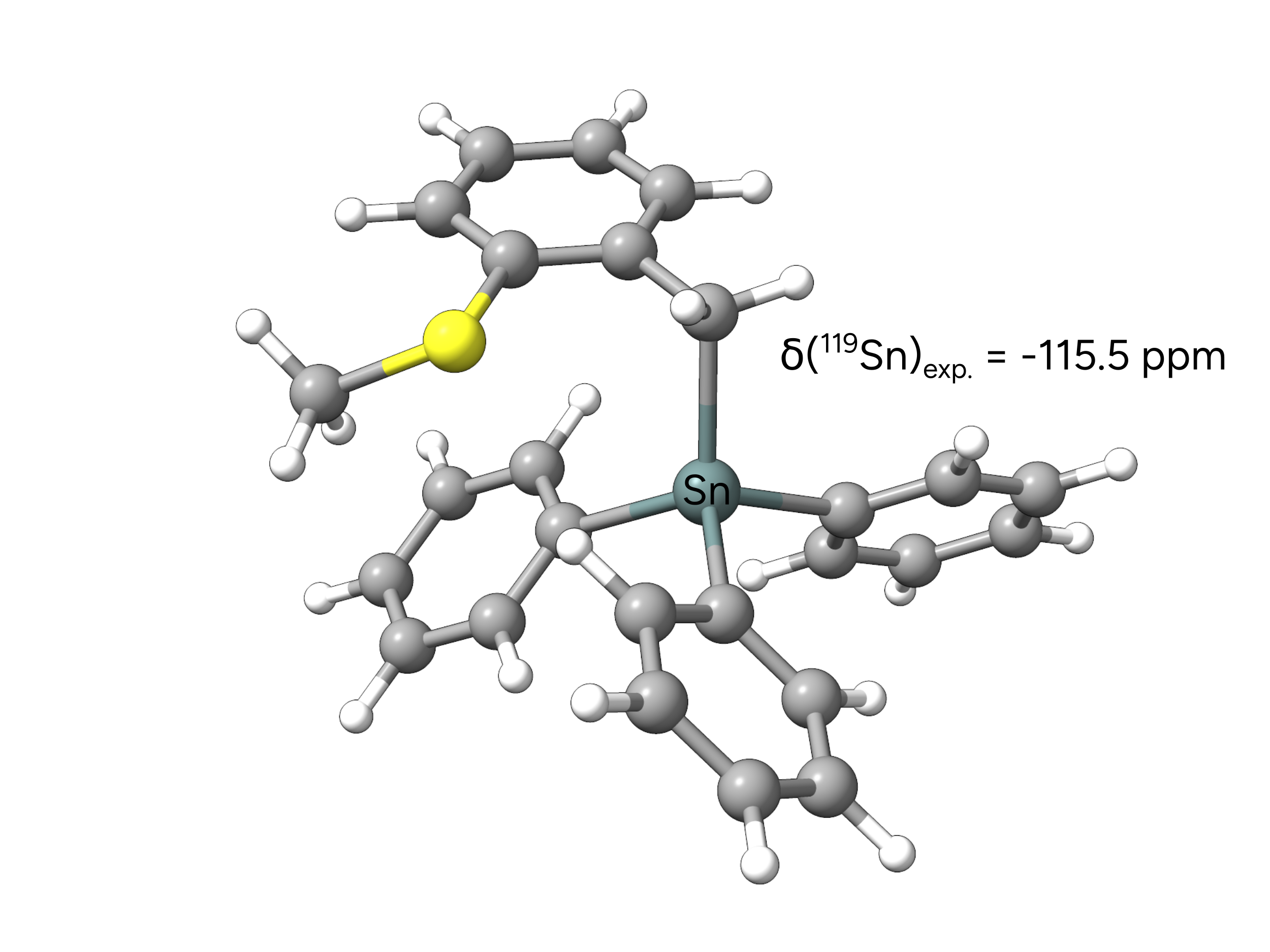
Respective inputs are:

!B97M-V X2C X2C-TZVPALL RIJDX X2C/J

*XYZFILE 0 1 structure.xyz

%eprnmr
  Nuclei = all Sn {shift}
end

!B97M-V ZORA ZORA-DEF2-TZVP RIJDX AUTOAUX

%basis
NewGTO Sn "SARC-ZORA-TZVP" end
end

*XYZFILE 0 1 structure.xyz

%eprnmr
  Nuclei = all Sn {shift}
end

!B97M-V ZORA DKH-DEF2-TZVP RIJDX AUTOAUX

%basis
NewGTO Sn "SARC-DKH-TZVP" end
end

*XYZFILE 0 1 structure.xyz

%eprnmr
  Nuclei = all Sn {shift}
end

Note

Note that if your desired basis set for the nucleus of interest is not available for all elements in the molecule, you can define individual basis sets.

If we now calculate the approximated chemical shift as described in the NMR spectroscopy tutorial, we obtain following values:

Calculated δ(¹¹⁹Sn) chemical shifts.#
Relativistic treatment	δ(¹¹⁹Sn) / ppm
ECP	-6.0
ZORA	-137.4
DKH2	-140.5
X2C	-169.8
Exp.	-115.5

Here, we see that employing an effective core potential (ECP) at the tin nucleus yields very bad results compared to the experiment. All other scalar-relativistic approaches yield reasonable agreement with the experiment considering the lack of spin-orbit coupling and environmental effects in our calculations.

Relativistic corrections#

Effective Core Potentials (ECPs)#

Scalar Relativistic Hamiltonians (ZORA/DKH/X2C)#

RI and ZORA/DKH/X2C#

Example 1: the Hg dimer#

Example 2: 119Sn NMR#

Structures Example 2#

Example 2: ¹¹⁹Sn NMR#