Local Energy Decomposition (LED)#

Decomposition of interaction energies in physically motivated components can be very useful to understand and control interaction patterns of different molecules. The local energy decomposition (LED) approach based on DLPNO-CCSD(T) interaction energies available within ORCA is one of the most sophisticated ones available.

\[\Delta E_{int.} = \Delta E_{el-prep}^{ref.} + E_{elstat}^{ref.} + E_{exch}^{ref.} + \Delta E^{C-CCSD}_{non-dispersion} + E^{C-CCSD}_{dispersion} + \Delta E^{C-(T) }_{int}\]

Often, the geometry relaxation upon coordination is additionally considered as \Delta E_{geo-prep}. This contribution is also known as strain. For more information on the interpretation and physical meaning of the LED contributions refer to the ORCA manual and refs. [Bistoni2020c][Bistoni2021].

Example: Alkane coordination in CpRe(CO)₂(n-pentane)#

As an example, we will decompose the interaction energy of n-pentane in CpRe(CO)₂(n-pentane).

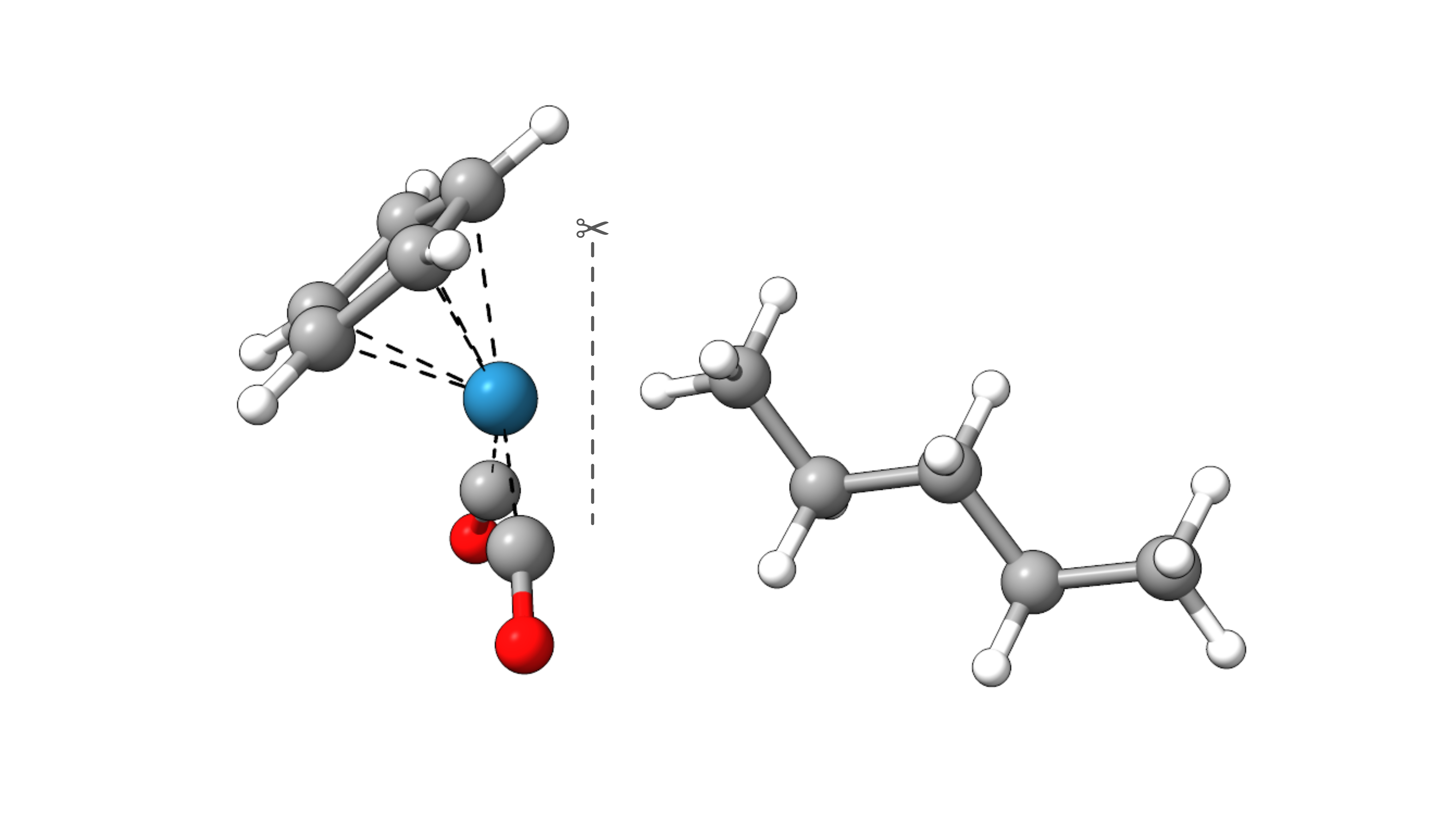
The LED analysis can be envoked by the simple input keyword LED. Further, the fragments CpRe(CO)₂ (1) and n-pentane (2) can be defined in the input file:

!DLPNO-CCSD(T) DEF2-SVP DEF2-SVP/C DEF2/J RIJCOSX VERYTIGHTSCF TIGHTPNO LED

*XYZ 0 1
C(1) -4.46463 -0.12110 0.22162
[...]
O(1) -0.99391 0.49487 -2.78478
C(2) 0.15487 -0.43421 0.93360
[...]
H(2) 5.37983 -0.86517 1.10337
*

Important

Note that in practice, basis sets of triple-zeta quality or larger are recommended.

This calculation will give you a summary of the LED analysis with all energies in atomic units:

-------------------------------------------------
FINAL SUMMARY DLPNO-CCSD ENERGY DECOMPOSITION (Eh)
-------------------------------------------------
  
Intrafragment REF. energy:                        
Intra fragment   1 (REF.)              -494.831813945     
Intra fragment   2 (REF.)              -196.014025982     
  
Interaction of fragments  2 and  1:    
Electrostatics (REF.)                  -0.191882846 
Exchange (REF.)                        -0.064165214
Dispersion (strong pairs)              -0.015692655
Dispersion (weak pairs)                -0.001188738 

Sum of non dispersive correlation terms: 
Non dispersion (strong pairs)          -2.466916428
Non dispersion (weak pairs)            -0.001534781

From this output, we can directly extract three of the contributions:

\[ E_{elstat}^{ref.} = \text{Electrostatics (REF.)} = -0.191882846 \]

\[ E_{exch}^{ref.} = \text{Exchange (REF.)} = -0.064165214 \]

\[ E^{C-CCSD}_{dispersion} = \text{Dispersion (strong pairs)} + \text{Dispersion (weak pairs)} = -0.001188738 \]

For the other three terms, we need additional calculations at the same level for the isolated fragments in the complex geometry.

For CpRe(CO)₂ (1):

!DLPNO-CCSD(T) DEF2-SVP DEF2-SVP/C DEF2/J RIJCOSX VERYTIGHTSCF TIGHTPNO LED

*XYZ 0 1
C(1) -4.46463 -0.12110 0.22162
[...]
O(1) -0.99391 0.49487 -2.78478

and for n-pentane (2):

!DLPNO-CCSD(T) DEF2-SVP DEF2-SVP/C DEF2/J RIJCOSX VERYTIGHTSCF TIGHTPNO

*XYZ 0 1
C(2) 0.15487 -0.43421 0.93360
[...]
H(2) 5.37983 -0.86517 1.10337
*

These calculations will give you essential parts needed to calculate the remaining contributions: E(0), E(CORR)(corrected), and Triples Correction (T):

The respective parts of the output for CpRe(CO)₂ (1) look like:

E(0)                                       ...   -494.901124578
E(CORR)(strong-pairs)                      ...     -1.652880437
E(CORR)(weak-pairs)                        ...     -0.001184807
E(CORR)(corrected)                         ...     -1.654065244
E(TOT)                                     ...   -496.555189821

Triples Correction (T)                     ...     -0.071314084
Final correlation energy                   ...     -1.725379328
E(CCSD)                                    ...   -496.555189821
E(CCSD(T))                                 ...   -496.626503906

and for n-pentane (2) like:

E(0)                                       ...   -196.190105836
E(CORR)(strong-pairs)                      ...     -0.806038024
E(CORR)(weak-pairs)                        ...     -0.000302952
E(CORR)(corrected)                         ...     -0.806340975
E(TOT)                                     ...   -196.996446812

Triples Correction (T)                     ...     -0.022482309
Final correlation energy                   ...     -0.828823285
E(CCSD)                                    ...   -196.996446812
E(CCSD(T))                                 ...   -197.018929121

With these data, we can now calculate the missing LED contributions:

\[\begin{split} \begin{split} \Delta E_{el-prep}^{ref.} & = [\text{Intra fragment 1 (REF.)} - \text{E(0)}_{frag 1}] + [\text{Intra fragment 2 (REF.)} - \text{E(0)}_{frag 2}] \\ & = 0.245390487 \end{split} \end{split}\]

\[\begin{split} \begin{split} \Delta E^{C-CCSD}_{non-dispersion} & = (\text{non-dispersion (strong pairs)} + \text{non-dispersion (weak pairs)}) \\ & - (\text{E(CORR)(corrected)}_{frag 1} + \text{E(CORR)(corrected)}_{frag 2}) \\ & = -0.008044990 \end{split} \end{split}\]

\[\begin{split} \begin{split} \Delta E^{C-(T) }_{int} & = \text{Triples Correction (T)}_{complex} \\ & - (\text{Triples Correction (T)}_{frag 1} + \text{Triples Correction (T)}_{frag 2}) \\ & = -0.002667311 \end{split} \end{split}\]

Now, we have all components of the LED analysis of the interaction energy of the fragments:

\(\Delta E_{int.}\)	\(\Delta E_{el-prep}^{ref.}\)	\(E_{elstat}^{ref.}\)	\(E_{exch}^{ref.}\)	\(\Delta E^{C-CCSD}_{non-disp.}\)	\(E^{C-CCSD}_{disp.}\)	\(\Delta E^{C-(T)}_{int}\)	Sum
a.u.	0.24539	-0.19188	-0.06417	-0.00804	-0.01688	-0.00267	-0.03825
kcal/mol	153.98	-120.41	-40.26	-5.05	-10.59	-1.67	-24.00

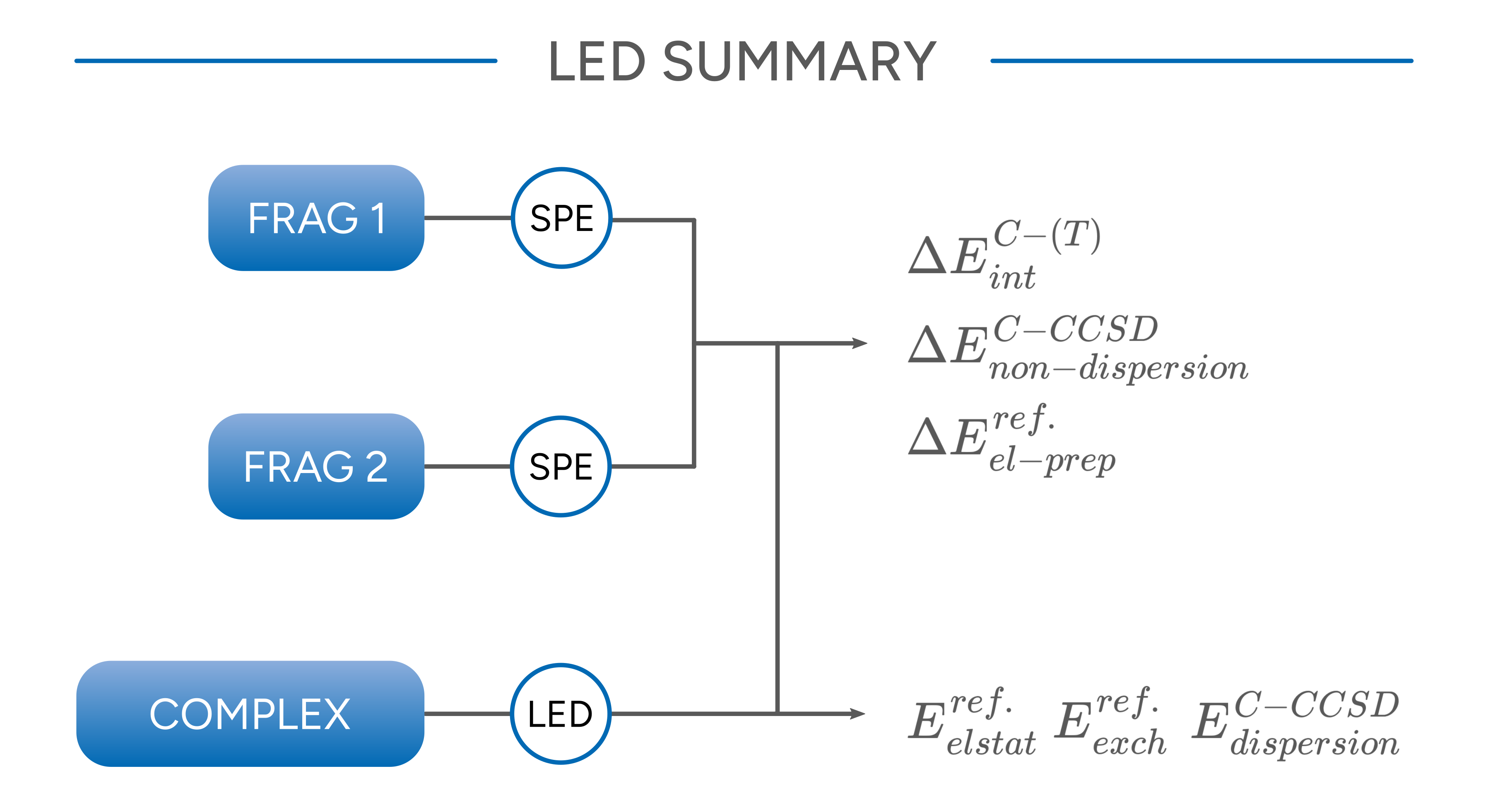
All six contributions sum up to the overall interaction energy that is also obtained from subtracting the total energies of the fragments from that of the complex. The following graphics summarizes the steps that have to be performed and from which calculation data are needed to calculate the individual components.

Dispersion Interaction Density (DID)#

Since London dispersion interactions are a crucial component of the interaction energy, understanding and controlling them became an integral part of modern compound design. For example, the concept of dispersion-energy-donors (DED).[Grimme2006][Grimme2011c][Schreiner2015] became particularly useful in this context. One way to visualize the London dispersion component of the LED analysis is the Dispersion Interaction Density (DID) plot.[Mata2016][Bistoni2019]
To obtain the DID, you can simply add %mdci DoDIDplot true end to your LED input and run the calculation as described before.

After a successful calculation, the DID will be stored in the basename.densities container as basename.ded21.

We can now use orca_plot to create a plotable datafile from the DID. To open the interactive interface call

orca_plot basename.gbw -i

Here, we now choose 1 - Enter type of plot to decide what to plot

PlotType       ... MO-PLOT
MO/Operator    ... 0 0
Output file    ... (null)
Format         ... Grid3d/Cube
Resolution     ... 40 40 40
Boundaries     ...   -16.680972    18.410507 (x direction)
                     -12.311453    12.849005 (y direction)
                     -12.262472    11.601143 (z direction)

       1 - Enter type of plot
       2 - Enter no of orbital to plot
       3 - Enter operator of orbital (0=alpha,1=beta)
       4 - Enter number of grid intervals
       5 - Select output file format
       6 - Plot CIS/TD-DFT difference densities
       7 - Plot CIS/TD-DFT transition densities
       8 - Set AO(=1) vs MO(=0) to plot
       9 - List all available densities

      10 - Generate the plot
      11 - exit this program
Enter a number: 1

From the given list, we now chose 15 - LED dispersion interaction density (ded21) which is also highlighted as available

-   molecular orbitals                          
-   (scf) electron density         ......  (scfp     )  - available
-   (scf) spin density             ......  (scfr     )  - NOT available
[...]
-   LED dispersion interaction density     (ded21    )  - available
-   Atom pair density                           
-   Shielding Tensors                           
-   Polarisability Tensor                       
-   AutoCI relaxed density         ......  (autocipre)  - NOT available
-   AutoCI unrelaxed density       ......  (autocipur)  - NOT available
-   AutoCI relaxed spin density    ......  (autocirre)  - NOT available
-   AutoCI unrelaxed spin density  ......  (autocirur)  - NOT available
Enter Type: 15

Now, the program will ask you if the suggested default basename.def21density file is the correct one, which we confirm

The default name of the density would be: led.ded21
Is this the one you want (y/n)? y

Via the options 5 - Select output file format we can further choose the format of the output file, in this case Gaussian cube, and via 4 - Enter number of grid intervals and the number of grid points that may be included. 10 - Generate the plot will then create the basename.eldens.cube file. This file now containes the data of the DID that finally may be rendered onto the simple electron density. The respective electron density can be created in the same way by simply choosing 2 - (scf) electron density instead.

These files can now be used to render the DID plot, for example with ChimeraX. On the left, you see the DID (isovalue = 0.12 kJ/mol/bohr³) and on the right the DID mapped to the electron density.

From the DID plot, we can easily see which parts of the fragments contribute most to the dispersion component of the interaction energy.

Local Energy Decomposition (LED)#

Example: Alkane coordination in CpRe(CO)2(n-pentane)#

Dispersion Interaction Density (DID)#

Starting structure#

Example: Alkane coordination in CpRe(CO)₂(n-pentane)#