Vibrational frequencies¶
After performing a Geometry optimization, you might want to compute the vibrational frequency of your system and plot normal mode animations. Here is how to do it, using the acetic acid as an example:
Frequencies¶
In order to first compute the frequencies, e.g. using DFT and the B3LYP functional use:
!B3LYP DEF2-SVP OPT FREQ
* XYZ 0 1
C -0.81589 -0.51571 -0.02512
C 0.30690 0.49327 -0.06114
H -0.42809 -1.56713 -0.28060
H -1.26914 -0.51520 1.06962
H -1.64631 -0.14518 -0.75104
O 0.16587 1.68279 -0.21470
O 1.51380 -0.07303 0.21899
H 2.16801 0.64625 0.13143
*
or one can also do that immediately after an optimization run using:
!B3LYP DEF2-SVP OPT FREQ
* XYZFILE 0 1 guess_aceticacid.xyz
and a geometry optimization will be performed. In case of success, it will be followed by the frequency calculation. When the computation of the Hessian matrix starts, a header will be printed:
-------------------------------------------------------------------------------
ORCA SCF HESSIAN
-------------------------------------------------------------------------------
Hessian of the Kohn-Sham DFT energy:
Kohn-Sham wavefunction type ... RKS
Hartree-Fock exchange scaling ... 0.200
Number of operators ... 1
Number of atoms ... 8
Basis set dimensions ... 76
Integral neglect threshold ... 2.5e-11
Integral primitive cutoff ... 2.5e-12
followed by the calculation of all of the necessary terms. After it is completed, one will directly see the vibrational frequencies in \(cm^{-1}\):
-----------------------
VIBRATIONAL FREQUENCIES
-----------------------
Scaling factor for frequencies = 1.000000000 (already applied!)
0: 0.00 cm**-1
1: 0.00 cm**-1
2: 0.00 cm**-1
3: 0.00 cm**-1
4: 0.00 cm**-1
5: 0.00 cm**-1
6: 82.29 cm**-1
7: 424.53 cm**-1
8: 544.40 cm**-1
9: 593.63 cm**-1
[...]
The first few frequencies are always zero, for they correspond to the rotational and translational modes. They should be five for linear molecules and six for non-linear molecules, the rest are corresponding to actual vibrational modes.
Scaling frequencies¶
In case you want to multiply all your frequency values by some number after the thermodynamic functions are computed, you can use:
%FREQ SCALFREQ 1.035 END
and all frequencies would be multiplied by 1.035.
Important
Always check your vibrational frequencies. If your geometry is a minimum, there should be no negative frequencies; if it is a transition state, there must be only one.
Visualizing normal modes¶
The vibrational modes can be animated Using Avogadro as a GUI. First, open the basename.out file, and you should see a panel on the right, such as:
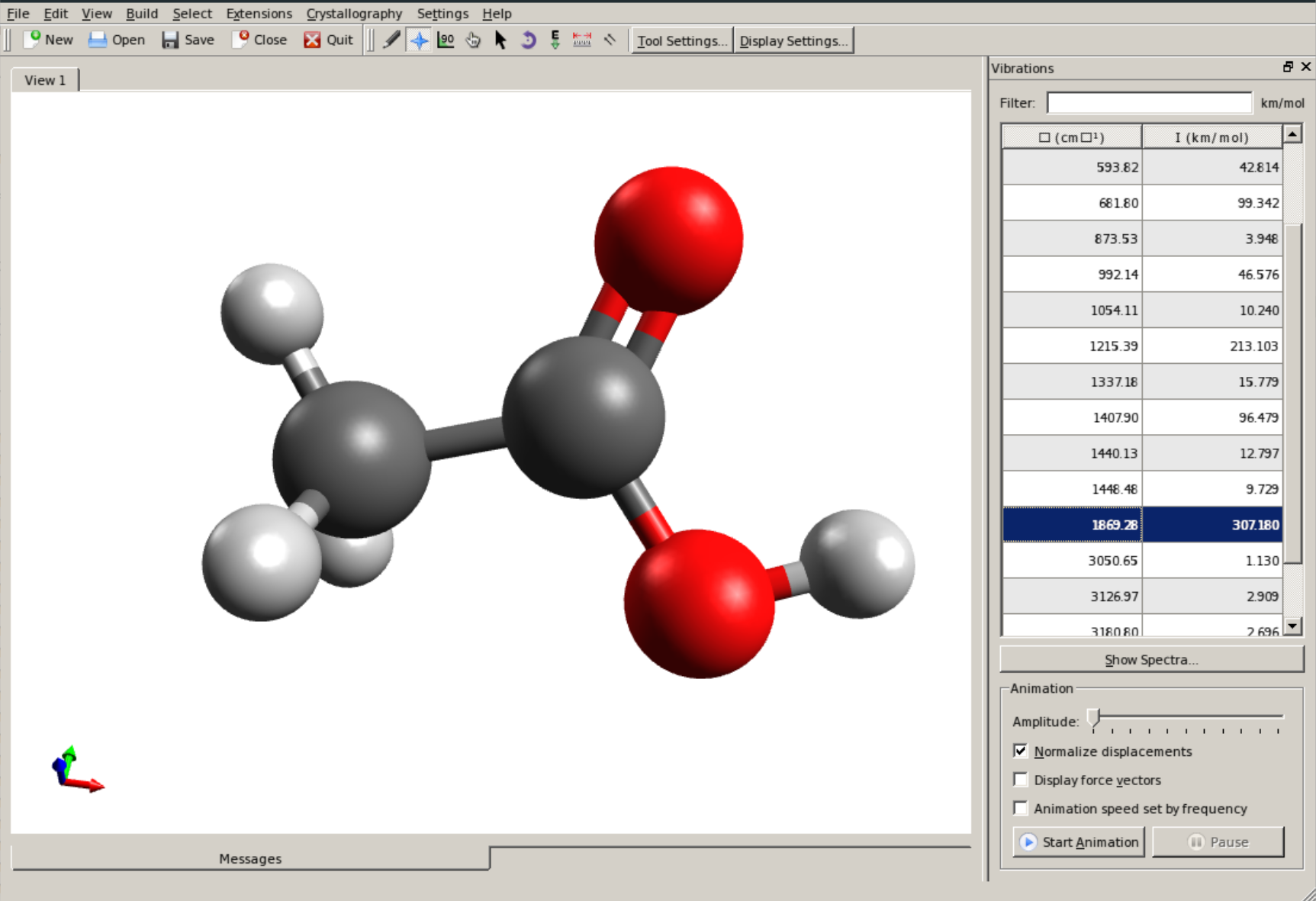
There you can select a frequency and click "Animate" to see how exactly is the mode that corresponds to that frequency. If one clicks at the mode at about \(\sim 1800 cm^{-1}\), which is expected to be a C=O stretching mode from classical organic chemistry, one sees:
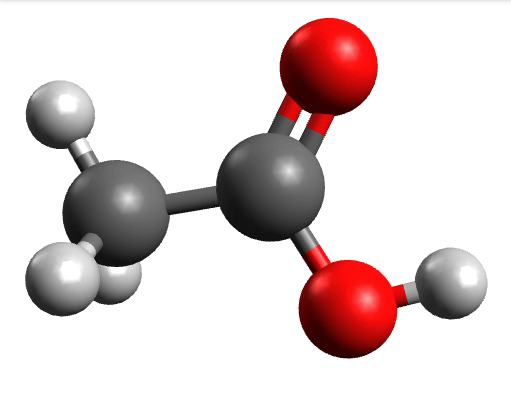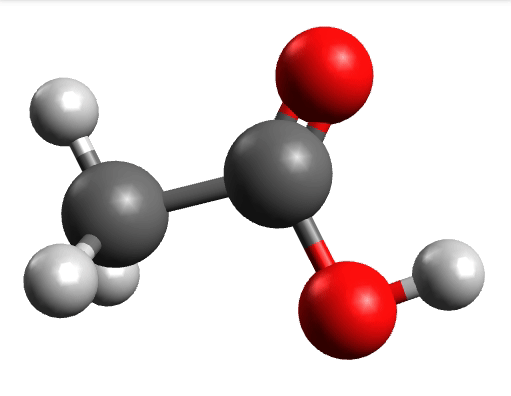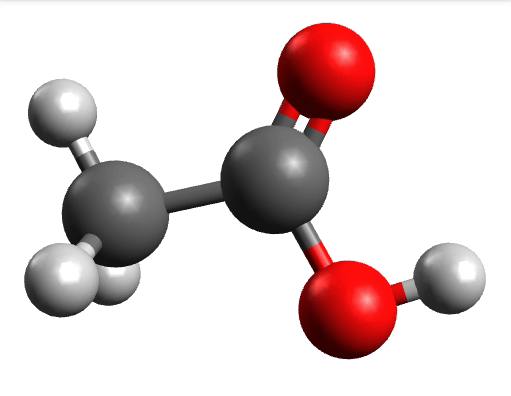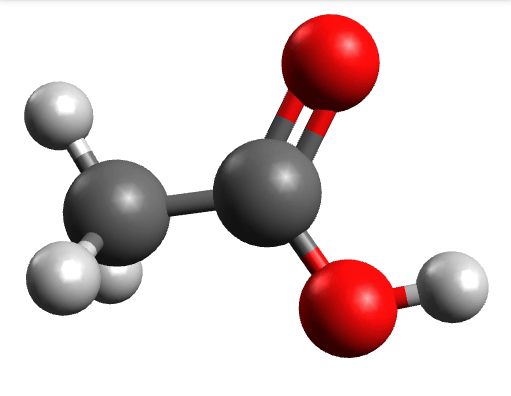
which corresponds to the classical prediction. The same applies for the other modes, e.g, the one at \(\sim 3150 cm^{-1}\), normally assigned as C-H stretchings:
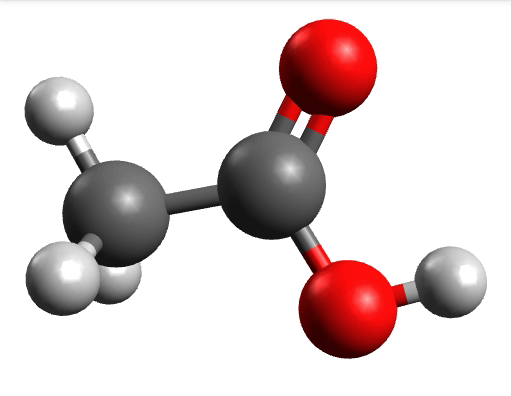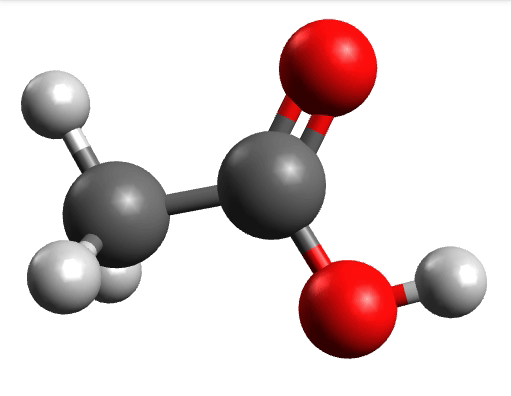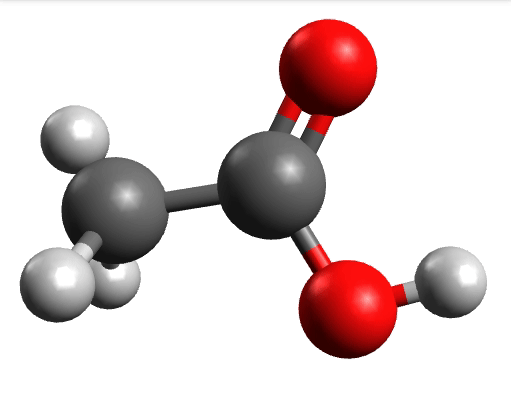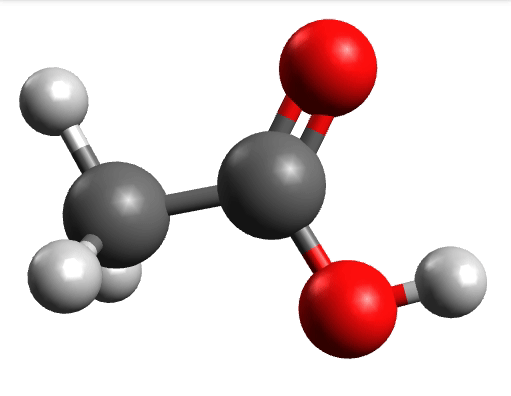
Removing negative frequencies¶
After your calculation, if there is one or more negative frequencies, that means your structure is not on a minimum. Here is an input for acetic acid that would result in such a situation:
!B3LYP DEF2-SVP OPT FREQ
* XYZ 0 1
C -8.23508 1.75252 -0.00446
C -6.80437 2.18360 0.03487
H -8.30301 0.65382 -0.15041
H -8.75566 2.25995 -0.84350
H -8.73273 2.02013 0.95115
O -6.52860 3.36373 0.18904
O -5.82021 1.26961 -0.09983
H -4.88856 1.53058 -0.07686
*
After optimizing and computing the frequencies, one gets:
-----------------------
VIBRATIONAL FREQUENCIES
-----------------------
Scaling factor for frequencies = 1.000000000 (already applied!)
0: 0.00 cm**-1
1: 0.00 cm**-1
2: 0.00 cm**-1
3: 0.00 cm**-1
4: 0.00 cm**-1
5: 0.00 cm**-1
6: -85.00 cm**-1 ***imaginary mode***
7: 430.96 cm**-1
8: 550.70 cm**-1
9: 590.13 cm**-1
with a so-called imaginary mode, meaning the geometry actually converged to a saddle point and a movement along the direction of that mode reduces the energy of the molecule.
One way to solve this is to open the output in Avogadro, click on the \(-85.0 cm^{-1}\) negative frequency and "Animate", to get:
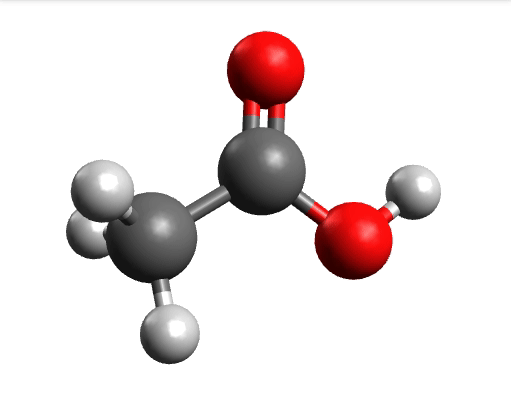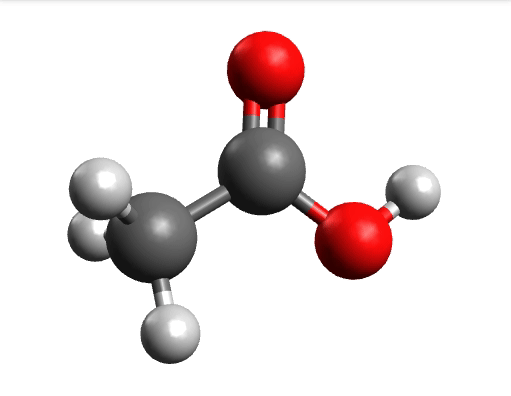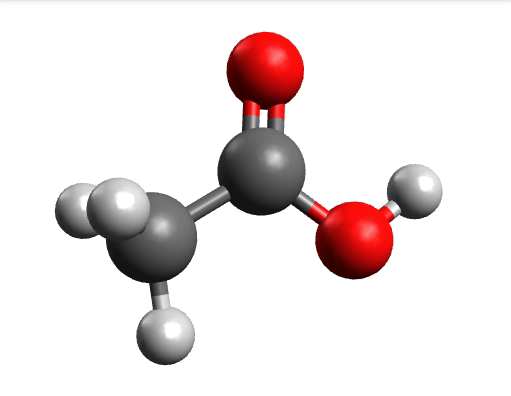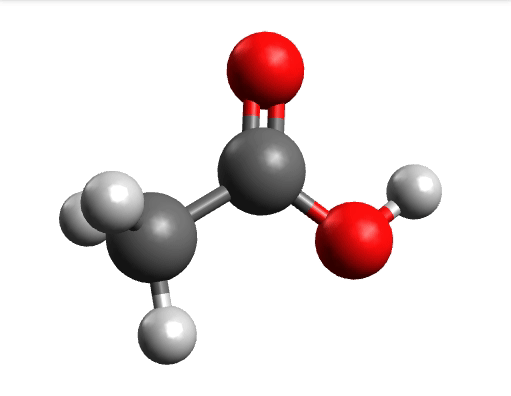
Now if you click "Pause" while the molecule is displaced, you will obtain a geometry further away from the saddle point. One can then save these coordinates and restart the calculation that finally converges to the minimum:
!B3LYP DEF2-SVP OPT FREQ
* XYZFILE 0 1 displaced_acetic.xyz
Numerical Frequencies¶
The computation of the Hessian matrix is not available for all methods in ORCA, but one can always do a numerical Hessian calculation, using the NUMFREQ keywords, such as:
!RI-B2PLYP DEF2-SVP DEF2-SVP/C NUMFREQ
and the Hessian will be computed by the central differences approach, after \(6N\) displacements, where \(N\) is the number of atoms in your system. This can be fully parallelised and sometimes is actually a better option than the analytical FREQ calculation, depending on your memory.
Restarting NUMFREQ calculations¶
These calculations can take a long time if one has a large system or a heavier method. In case anything happens and the calculation ends, it can be restarted using:
!RI-B2PLYP DEF2-SVP DEF2-SVP/C NUMFREQ
%FREQ RESTART TRUE END
If the basename.hess file is present on the same folder as the input, the computation will be restarted from where stopped.
Important
There are many extra options for %FREQ, please check the ORCA manual for more info.